面试经典 150 题-图

LeetCode 面试经典 150 题-图

岛屿数量

深度优先搜索

1. 遍历图，当遇到为1的格子时，开始深度优先搜索。
2. 判断当前位置是否合法，判断是否是1防止重复遍历。
3. 标记当前位置已访问过，然后遍历上下左右四个方向。

class Solution {
    public int numIslands(char[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int ans = 0;

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == '1') {
                    ans++;
                    dfs(grid, i, j);
                }
            }
        }

        return ans;
    }

    private void dfs(char[][] grid, int row, int col) {
        // 判断位置是否合法
        if (!isValid(grid, row, col)) {
            return;
        }
        // 防止重复遍历
        if (grid[row][col] != '1') {
            return;
        } 
        // 标记已访问过
        grid[row][col] = '2';
        // 遍历上下左右四个方向
        dfs(grid, row - 1, col);
        dfs(grid, row + 1, col);
        dfs(grid, row, col - 1);
        dfs(grid, row, col + 1);
    }

    private boolean isValid(char[][] grid, int row, int col) {
        int m = grid.length;
        int n = grid[0].length;
        if (row >= 0 && row < m && col >= 0 && col < n ) {
            return true;
        }
        return false;
    }
}

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

广度优先搜索

1. 遍历图，如果一个位置为 1，则将其加入队列，开始进行广度优先搜索。
2. 在广度优先搜索的过程中，每个搜索到的 1 都会被标记为 2。
3. 直到队列为空，搜索结束。最终岛屿的数量就是我们进行广度优先搜索的次数。

class Solution {
    public int numIslands(char[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int ans = 0;

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == '1') {
                    ans++;
                    grid[i][j] = '2';
                    // 定义队列
                    Queue<Integer> neighbors = new LinkedList<>();
                    neighbors.offer(i * n + j);
                    // 广度优先搜索
                    while (!neighbors.isEmpty()) {
                        int id = neighbors.poll();
                        int r = id / n;
                        int c = id % n;
                        if (isValid(grid, r - 1, c) && grid[r - 1][c] == '1') {
                            neighbors.offer((r-1) * n + c);
                            grid[r-1][c] = '2';
                        }
                        if (isValid(grid, r + 1, c) && grid[r + 1][c] == '1') {
                            neighbors.offer((r+1) * n + c);
                            grid[r+1][c] = '2';
                        }
                        if (isValid(grid, r, c - 1) && grid[r][c - 1] == '1') {
                            neighbors.offer(r * n + c - 1);
                            grid[r][c-1] = '2';
                        }
                        if (isValid(grid, r, c + 1) && grid[r][c + 1] == '1') {
                            neighbors.offer(r * n + c + 1);
                            grid[r][c+1] = '2';
                        }
                    }
                }
            }
        }

        return ans;
    }

    private boolean isValid(char[][] grid, int row, int col) {
        int m = grid.length;
        int n = grid[0].length;
        if (row >= 0 && row < m && col >= 0 && col < n ) {
            return true;
        }
        return false;
    }
}

• 时间复杂度：O(mn)
• 空间复杂度：O(min(m, n))

并查集

如果一个位置为 1，则将其与相邻四个方向上的 1 在并查集中进行合并。最终岛屿的数量就是并查集中连通分量的数目。

1. 并查集成员变量：父亲数组、秩数组、连通集数量。
2. 并查集成员函数：
   • 构造函数：初始化父亲数组和秩数组。
   • find函数：查找祖先。
   • unite函数：按秩合并两个结点。
   • getCount函数：返回count。

class Solution {
    class UnionFind {
        int count;
        int[] parent;
        int[] rank;

        public UnionFind(char[][] grid) {
            count = 0;
            int m = grid.length;
            int n = grid[0].length;
            parent = new int[m * n];
            rank = new int[m * n];
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    if (grid[i][j] == '1') {
                        parent[i * n + j] = i * n + j;
                        ++count;
                    }
                    rank[i * n + j] = 0;
                }
            }
        }

        public int find(int i) {
            if (parent[i] != i) {
                parent[i] = find(parent[i]);
            }
            return parent[i];
        }

        public void union(int x, int y) {
            int rootx = find(x);
            int rooty = find(y);
            if (rootx != rooty) {
                if (rank[rootx] > rank[y]) {
                    parent[rooty] = parent[x];
                } else if (rank[rootx] < rank[rooty]) {
                    parent[rootx] = parent[y];
                } else {
                    parent[rooty] = rootx;
                    rank[rootx]++;
                }
                --count;
            }
        }

        public int getCount() {
            return count;
        }
    }

    public int numIslands(char[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int ans = 0;

        UnionFind uf = new UnionFind(grid);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == '1') {
                    grid[i][j] = '2';
                    if (isValid(grid, i-1, j) && grid[i-1][j] == '1') {
                        uf.union(i * n + j, (i-1) * n + j);
                    }
                    if (isValid(grid, i+1, j) && grid[i+1][j] == '1') {
                        uf.union(i * n + j, (i+1) * n + j);
                    }
                    if (isValid(grid, i, j-1) && grid[i][j-1] == '1') {
                        uf.union(i * n + j, i * n + j - 1);
                    }
                    if (isValid(grid, i, j+1) && grid[i][j+1] == '1') {
                        uf.union(i * n + j, i * n + j + 1);
                    }
                }
            }
        }

        return uf.getCount();
    }

    private boolean isValid(char[][] grid, int row, int col) {
        int m = grid.length;
        int n = grid[0].length;
        if (row >= 0 && row < m && col >= 0 && col < n ) {
            return true;
        }
        return false;
    }
}

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

被围绕的区域

深度优先搜索

• 对于每一个边界上的 O，我们以它为起点，标记所有与它直接或间接相连的字母 O；
• 最后我们遍历这个矩阵，对于每一个字母：
  • 如果该字母被标记过，则该字母为没有被字母 X 包围的字母 O，我们将其还原为字母 O；
  • 如果该字母没有被标记过，则该字母为被字母 X 包围的字母 O，我们将其修改为字母 X。

class Solution {
    public void solve(char[][] board) {
        int m = board.length;
        int n = board[0].length;

        // 第一列和最后一列
        for (int i = 0; i < m; i++) {
            dfs(board, i, 0);
            dfs(board, i, n - 1);
        }    
        // 第一行和最后一行
        for (int i = 0; i < n; i++) {
            dfs(board, 0, i);
            dfs(board, m - 1, i);
        }
        // 修改标记
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }
    }

    public void dfs(char[][] board, int row, int col) {
        int m = board.length;
        int n = board[0].length;

        // 检查边界
        if (row < 0 || row >= m || col < 0 || col >= n) {
            return;
        }

        // 如果是'O'，则标记为'A'
        if (board[row][col] == 'O') {
            board[row][col] = 'A';
            // 递归上下左右
            dfs(board, row - 1, col);
            dfs(board, row + 1, col);
            dfs(board, row, col - 1);
            dfs(board, row, col + 1);
        }
    }
}

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

克隆图

深度优先搜索

1. 使用一个哈希表存储所有已被访问和克隆的节点。哈希表中的 key 是原始图中的节点，value 是克隆图中的对应节点。
2. 从给定节点开始遍历图。如果某个节点已经被访问过，则返回其克隆图中的对应节点。
3. 如果当前访问的节点不在哈希表中，则创建它的克隆节点并存储在哈希表中。注意：在进入递归之前，必须先创建克隆节点并保存在哈希表中。如果不保证这种顺序，可能会在递归中再次遇到同一个节点，再次遍历该节点时，陷入死循环。
4. 递归调用每个节点的邻接点。每个节点递归调用的次数等于邻接点的数量，每一次调用返回其对应邻接点的克隆节点，最终返回这些克隆邻接点的列表，将其放入对应克隆节点的邻接表中。这样就可以克隆给定的节点和其邻接点。

class Solution {
    private HashMap<Node, Node> visited = new HashMap<>();

    public Node cloneGraph(Node node) {
        // 边界条件
        if (node == null) {
            return node;
        }    

        // 如果已经访问过，则可以直接返回
        if (visited.containsKey(node)) {
            return visited.get(node);
        }

        // 克隆节点
        Node cloneNode = new Node(node.val, new ArrayList());
        visited.put(node, cloneNode);

        // 克隆邻居节点
        for (Node neighbor : node.neighbors) {
            cloneNode.neighbors.add(cloneGraph(neighbor));
        }

        return cloneNode;
    }
}

• 时间复杂度：O(n)
• 空间复杂度：O(n)

广度优先搜索

1. 使用一个哈希表 visited 存储所有已被访问和克隆的节点。哈希表中的 key 是原始图中的节点，value 是克隆图中的对应节点。
2. 将题目给定的节点添加到队列。克隆该节点并存储到哈希表中。
3. 每次从队列首部取出一个节点，遍历该节点的所有邻接点。如果某个邻接点已被访问，则该邻接点一定在 visited 中，那么从 visited 获得该邻接点，否则创建一个新的节点存储在 visited 中，并将邻接点添加到队列。将克隆的邻接点添加到克隆图对应节点的邻接表中。重复上述操作直到队列为空，则整个图遍历结束。

class Solution {
    private HashMap<Node, Node> visited = new HashMap<>();

    public Node cloneGraph(Node node) {
        // 边界条件
        if (node == null) {
            return node;
        }    

        // 定义队列
        Queue<Node> queue = new LinkedList<Node>();
        queue.offer(node);
        visited.put(node, new Node(node.val, new ArrayList()));

        // 广度优先搜索
        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            for (Node neighbor : cur.neighbors) {
                if (!visited.containsKey(neighbor)) {
                    visited.put(neighbor, new Node(neighbor.val, new ArrayList()));
                    queue.offer(neighbor);
                }
                visited.get(cur).neighbors.add(visited.get(neighbor));
            }
        }

        return visited.get(node);
    }
}

• 时间复杂度：O(n)
• 空间复杂度：O(n)

除法求值

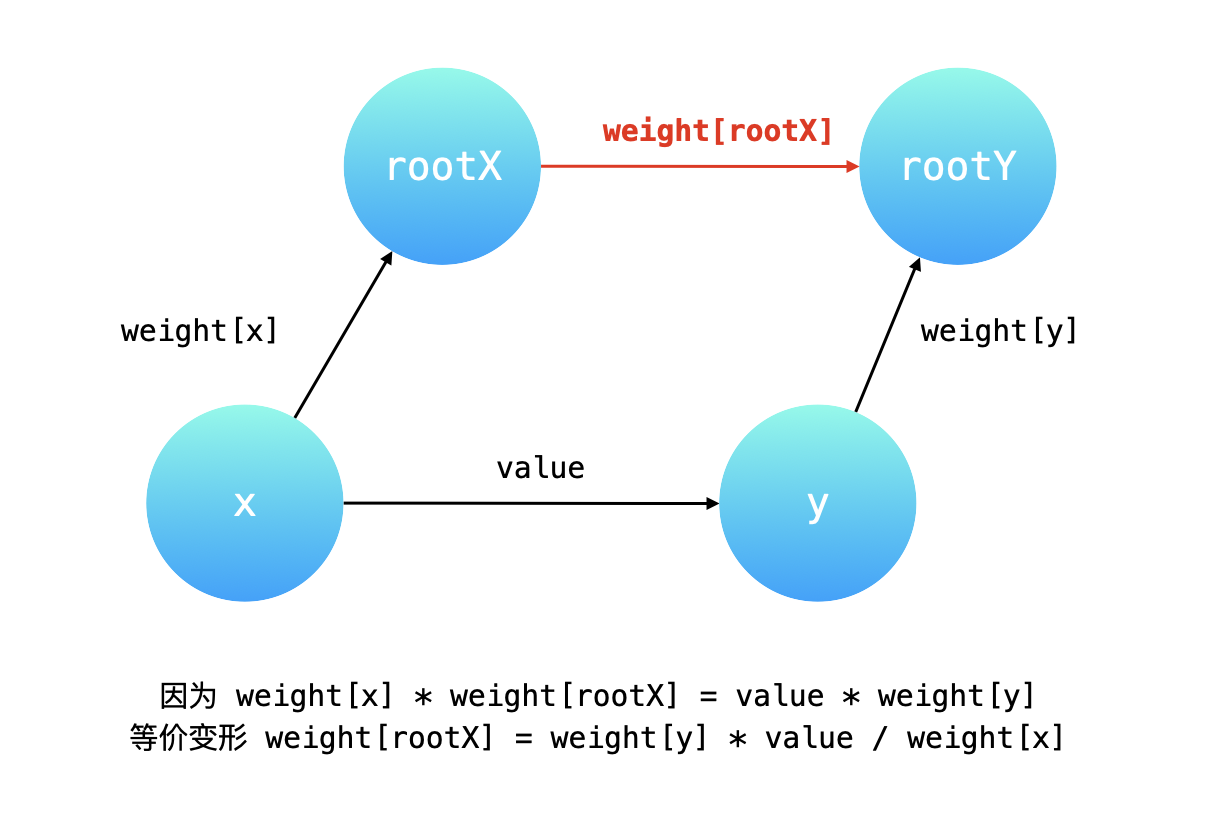
并查集

1. 定义并查集：
   • 父节点数组、权重数组（代表到父节点的权值）
   • 初始化：父节点为其本身下标，权重初始化为1.0
   • 合并：rootx的父亲指向rooty，并计算weight[rootx]；
     
   • 查找（路径压缩）：在查找根节点的同时更新每个节点的权值，保持了树的扁平化。
   • 查询是否连通：如果父节点相同，则连通，直接计算值；否则返回-1.
2. 将变量映射到整数，用哈希表存放。
3. 合并每个equation。
4. 查询。

class Solution {
    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
        // 最多有2 * equationsSize个id
        int equationsSize = equations.size();
        UnionFind uf = new UnionFind(2 * equationsSize);
        // 预处理，将变量与id映射
        Map<String, Integer> hash = new HashMap<>(2 * equationsSize);
        int id = 0;
        for (int i = 0; i < equationsSize; i++) {
            List<String> equation = equations.get(i);
            String var1 = equation.get(0);
            String var2 = equation.get(1);

            if (!hash.containsKey(var1)) {
                hash.put(var1, id);
                id++;
            }
            if (!hash.containsKey(var2)) {
                hash.put(var2, id);
                id++;
            }

            uf.union(hash.get(var1), hash.get(var2), values[i]);
        }

        // 查询
        int queriesSize = queries.size();
        double[] res = new double[queriesSize];
        for (int i = 0; i < queriesSize; i++) {
            String var1 = queries.get(i).get(0);
            String var2 = queries.get(i).get(1);

            Integer id1 = hash.get(var1);
            Integer id2 = hash.get(var2);

            if (id1 == null || id2 == null) {
                res[i] = -1.0;
            } else {
                res[i] = uf.isConnected(id1, id2);
            }
        }

        return res;
    }

    private class UnionFind {
        // 父节点数组和权值数组
        private int[] parent;
        private double[] weight;

        public UnionFind(int n) {
            parent = new int[n];
            weight = new double[n];
            for (int i = 0; i < n; i++) {
                parent[i] = i;
                weight[i] = 1.0;
            }
        }

        // 合并
        public void union(int x, int y, double value) {
            int rootx = find(x);
            int rooty = find(y);
            if (rootx == rooty) {
                return;
            }
            parent[rootx] = rooty;
            weight[rootx] = weight[y] * value / weight[x];
        }

        // 路径压缩
        public int find(int x) {
            if (x != parent[x]) {
                int orign = parent[x];
                parent[x] = find(parent[x]);
                weight[x] *= weight[orign];
            }
            return parent[x];
        }

        public double isConnected(int x, int y) {
            int rootx = find(x);
            int rooty = find(y);
            if (rootx == rooty) {
                return weight[x] / weight[y];
            } else {
                return -1.0;
            }
        }
    }
}

课程表

深度优先搜索

在每一轮的搜索搜索开始时，任取一个「未搜索」的节点开始进行深度优先搜索。

1. 将当前搜索的节点 u 标记为「搜索中」，遍历该节点的每一个相邻节点 v：
   • 如果 v 为「未搜索」，那么我们开始搜索 v，待搜索完成回溯到 u；
   • 如果 v 为「搜索中」，那么我们就找到了图中的一个环，因此是不存在拓扑排序的；
   • 如果 v 为「已完成」，那么说明 v 已经在栈中了，而 u 还不在栈中，因此 u 无论何时入栈都不会影响到 (u,v) 之前的拓扑关系，以及不用进行任何操作。
2. 当 u 的所有相邻节点都为「已完成」时，我们将 u 放入栈中，并将其标记为「已完成」。
3. 在整个深度优先搜索的过程结束后，如果我们没有找到图中的环，那么栈中存储这所有的 n 个节点，从栈顶到栈底的顺序即为一种拓扑排序。

class Solution {
    List<List<Integer>> edges;
    int[] visited;
    boolean valid = true;

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 初始化图
        edges = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            edges.add(new ArrayList<>());
        }
        visited = new int[numCourses];
        // 建图
        for (int[] info : prerequisites) {
            edges.get(info[1]).add(info[0]);
        }
        // 深度优先搜索
        for (int i = 0; i < numCourses && valid; i++) {
            if (visited[i] == 0) {
                dfs(i);
            }
        }
        return valid;
    }

    private void dfs(int u) {
        visited[u] = 1;
        // 遍历所有邻接节点
        for (int v : edges.get(u)) {
            if (visited[v] == 0) {
                dfs(v);
                if (!valid) {
                    return;
                }
            }else if (visited[v] == 1) {
                valid = false;
                return;
            }
        }
        // 回溯
        visited[u] = 2;
    }
}

• 时间复杂度：O(m+n)
• 空间复杂度：O(m+n)

广度优先搜索

1. 初始时，所有入度为 0 的节点都被放入队列中，它们就是可以作为拓扑排序最前面的节点，并且它们之间的相对顺序是无关紧要的。
2. 在广度优先搜索的每一步中，我们取出队首的节点 u：
   • 我们将 u 放入答案中；
   • 我们移除 u 的所有出边，也就是将 u 的所有相邻节点的入度减少 1。如果某个相邻节点 v 的入度变为 0，那么我们就将 v 放入队列中。
3. 在广度优先搜索的过程结束后。如果答案中包含了这 n 个节点，那么我们就找到了一种拓扑排序，否则说明图中存在环，也就不存在拓扑排序了。
4. 由于我们只需要判断是否存在一种拓扑排序，因此我们省去存放答案数组，而是只用一个变量记录被放入答案数组的节点个数。在广度优先搜索结束之后，我们判断该变量的值是否等于课程数，就能知道是否存在一种拓扑排序。

class Solution {
    List<List<Integer>> edges;
    int[] indeg;

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        // 初始化图
        edges = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            edges.add(new ArrayList<>());
        }
        indeg = new int[numCourses];
        // 建图
        for (int[] info : prerequisites) {
            edges.get(info[1]).add(info[0]);
            indeg[info[0]]++;
        }
        // 广度优先搜索
        Queue<Integer> queue = new LinkedList<Integer>();
        for (int i = 0; i < numCourses; i++) {
            if (indeg[i] == 0) {
                queue.offer(i);
            }
        }
        int visited = 0;
        while (!queue.isEmpty()) {
            visited++;
            int u = queue.poll();
            for (int v : edges.get(u)) {
                --indeg[v];
                if (indeg[v] == 0) {
                    queue.offer(v);
                }
            }
        }
        return visited == numCourses;
    }
}

• 时间复杂度：O(m + n)
• 空间复杂度：O(m + n)

课程表II

和上一题的不同在于，这里需要记录拓扑排序的路径。

深度优先搜索

class Solution {
    List<List<Integer>> edges;
    int[] visited;
    int[] res;
    boolean valid = true;
    int index;

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        // 初始化图
        edges = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            edges.add(new ArrayList<>());
        }
        visited = new int[numCourses];
        res = new int[numCourses];
        index = numCourses - 1;
        // 建图
        for (int[] info : prerequisites) {
            edges.get(info[1]).add(info[0]);
        }
        // 深度优先搜索
        for (int i = 0; i < numCourses && valid; i++) {
            if (visited[i] == 0) {
                dfs(i);
            }
        }
        // 返回结果
        if (!valid) {
            return new int[0];
        } 
        return res;
    }

    private void dfs(int u) {
        // 标记已访问过
        visited[u] = 1;

        // 遍历所有邻接节点
        for (int v : edges.get(u)) {
            if (visited[v] == 0) {
                dfs(v);
                if (!valid) {
                    return;
                }
            } else if (visited[v] == 1) {
                valid = false;
                return;
            }
        }

        // 标记已完成
        visited[u] = 2;
        // 加入结果
        res[index--] = u;
    }
}

• 时间复杂度：O(m + n)
• 空间复杂度：O(m + n)

广度优先搜索

class Solution {
    List<List<Integer>> edges;
    int[] indeg;
    int[] res;
    int index;

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        // 初始化图
        edges = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            edges.add(new ArrayList<>());
        }
        indeg = new int[numCourses];
        res = new int[numCourses];
        index = 0;

        // 建图
        for (int[] info : prerequisites) {
            edges.get(info[1]).add(info[0]);
            indeg[info[0]]++;
        }

        // 广度优先搜索
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (indeg[i] == 0) {
                queue.offer(i);
            }
        }
        int visited = 0;
        while (!queue.isEmpty()) {
            visited++;
            int u = queue.poll();
            res[index++] = u;
            // 对于所有邻接节点
            for (int v : edges.get(u)) {
                --indeg[v];
                if (indeg[v] == 0) {
                    queue.offer(v);
                }
            }
        }
        
        // 返回结果
        if (visited != numCourses) {
            return new int[0];
        } 
        return res;
    }
}

• 时间复杂度：O(m + n)
• 空间复杂度：O(m + n)

蛇梯棋

广度优先搜索

原问题等价于在有向图上求出从 1 到 $n^2$ 的最短路长度。

1. 抽象成有向图：
   • 不是蛇或梯子，添加x指向$x+i(0 \leq i \leq 6)$的边；
   • 是蛇或梯子，添加x指向y的边；
2. 将节点编号和到达该节点的移动次数作为搜索状态，顺着该节点的出边扩展新状态，直至到达终点，返回此时的移动次数。若无法到达终点则返回 −1。
   • 用一个队列来存储搜索状态，初始时将起点状态 (1,0) 加入队列，表示当前位于起点 1，移动次数为 0。
   • 不断取出队首，每次取出队首元素时扩展新状态，即遍历该节点的出边，若出边对应节点未被访问，则将该节点和移动次数加一的结果作为新状态，加入队列。
   • 如此循环直至到达终点或队列为空。
3. 需要计算出编号在棋盘中的对应行列，以便从 board 中得到目的地。设编号为 id，由于每行有 n 个数字，其位于棋盘从下往上数的第$r = \frac{id-1}{n}$行，由于棋盘的每一行会交替方向，若 r 为偶数，则编号方向从左向右，列号为 $(id−1) \mod n$；若 r 为奇数，则编号方向从右向左，列号为 $n - 1 - ((id - 1) \mod n)$。

class Solution {
    public int snakesAndLadders(int[][] board) {
        int n = board.length;
        // 标记编号是否已访问过
        boolean[] visited = new boolean[n * n + 1];
        // 队列，存储编号和次数
        Queue<int[]> queue = new LinkedList<>();
        queue.offer(new int[]{1, 0});
        // 广度优先搜索
        while (!queue.isEmpty()) {
            int[] point = queue.poll();
            // 搜索能到达的位置
            for (int i = 1; i <= 6; i++) {
                int next = point[0] + i;
                // 超出边界
                if (next > n * n) {
                    break;
                }
                // 计算下一步到达的位置
                int[] rc = id2rc(next, n);
                // 存在蛇或梯子
                if (board[rc[0]][rc[1]] > 0) {
                    next = board[rc[0]][rc[1]];
                }
                // 到达终点
                if (next == n * n) {
                    return point[1] + 1;
                }
                // 未访问过，加入队列
                if (!visited[next]) {
                    visited[next] = true;
                    queue.offer(new int[]{next, point[1] + 1});
                }
            }
        }
        return -1;
    }

    // id转换为行列
    public int[] id2rc(int id, int n) {
        int r = (id - 1) / n;
        int c = (id - 1) % n;
        if (r % 2 == 1) {
            c = n - 1 - c;
        }
        return new int[]{n - 1 - r, c};
    }
}

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n^2)$

最小基因变化

广度优先搜索

1. 定义两个哈希表存放基因库和基因序列是否访问过。
2. 定义队列，存放基因序列。
3. 广度优先搜索：
   • 弹出当前层基因序列，然后对其所有可能的24种变化做处理：
   • 如果变化到end，直接返回步数；
   • 否则加入队列，标记已访问过。

class Solution {
    public int minMutation(String startGene, String endGene, String[] bank) {
        // 定义哈希表存储基因库和标记
        Set<String> cnt = new HashSet<>();
        Set<String> visited = new HashSet<>();
        char[] keys = {'A', 'C', 'G', 'T'};
        for (String w : bank) {
            cnt.add(w);
        }
        // 特殊情况
        if (startGene.equals(endGene)) {
            return 0;
        }
        if (!cnt.contains(endGene)) {
            return -1;
        }
        // 定义队列
        Queue<String> queue = new LinkedList<>();
        queue.offer(startGene);
        visited.add(startGene);
        int step = 1;
        // 广度优先
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                String cur = queue.poll();
                for (int j = 0; j < 8; j++) {
                    for (int k = 0; k < 4; k++) {
                        // 基因变化
                        if (keys[k] != cur.charAt(j)) {
                            StringBuffer sb = new StringBuffer(cur);
                            sb.setCharAt(j, keys[k]);
                            // 没出现过且存在于基因库
                            String next = sb.toString();
                            if (!visited.contains(next) && cnt.contains(next)) {
                                // 变化到endGene
                                if (next.equals(endGene)) {
                                    return step;
                                }
                                queue.offer(next);
                                visited.add(next);
                            }
                        }
                    }
                }
            }
            step++;
        }
        return -1;
    }
}

• 时间复杂度：O(C×n×m)，其中 n 为基因序列的长度，m 为数组 bank 的长度。对于队列中的每个合法的基因序列每次都需要计算 C×n 种变化，在这里 C=4；队列中最多有 m 个元素，因此时间复杂度为 O(C×n×m)。
• 空间复杂度：O(n×m)，其中 n 为基因序列的长度，m 为数组 bank 的长度。合法性的哈希表中一共存有 m 个元素，队列中最多有 m 个元素，每个元素的空间为 O(n)；队列中最多有 m 个元素，每个元素的空间为 O(n)，因此空间复杂度为 O(n×m)。

预处理优化

1. 邻接表的构建：
   • adj[i] 存储与基因 bank[i] 相差一个字符的基因的索引。
   • 通过遍历 bank 中的基因对，比较每两个基因之间的差异，如果差异只有一个字符，就在它们之间建立连接。
2. 广度优先搜索（BFS）：
   • 在 BFS 中，我们从 start 基因出发，找到所有与它相差一个字符的基因，并将它们放入队列。
   • 之后从队列中取出基因，查找它的邻接基因，直到找到 end 基因，返回步数。
   • 如果队列为空，且未找到 end，则返回 -1，表示无法从 start 到达 end。

class Solution {
    // minMutation 方法：计算从 start 到 end 基因的最小变异步数
    public int minMutation(String start, String end, String[] bank) {
        int m = start.length();  // 基因字符串的长度
        int n = bank.length;  // 基因库的大小
        // 创建一个邻接表（图）adj，存储每个基因与其他基因的连接关系
        List<Integer>[] adj = new List[n];
        for (int i = 0; i < n; i++) {
            adj[i] = new ArrayList<Integer>();  // 初始化每个基因的邻接列表
        }

        int endIndex = -1;  // 记录 end 基因在基因库中的索引
        // 连接每对相差一个字符的基因
        for (int i = 0; i < n; i++) {
            if (end.equals(bank[i])) {
                endIndex = i;  // 找到 end 基因的索引
            }
            // 遍历所有基因库中的基因，查找与当前基因相差一个字符的基因
            for (int j = i + 1; j < n; j++) {
                int mutations = 0;  // 记录两个基因之间的字符差异数
                // 比较两个基因的每个字符
                for (int k = 0; k < m; k++) {
                    if (bank[i].charAt(k) != bank[j].charAt(k)) {
                        mutations++;  // 如果字符不同，差异数加1
                    }
                    if (mutations > 1) {
                        break;  // 如果差异数超过1，跳出循环
                    }
                }
                // 如果两个基因之间只有一个字符的差异，建立邻接关系
                if (mutations == 1) {
                    adj[i].add(j);  // 将 j 基因加入 i 基因的邻接列表
                    adj[j].add(i);  // 将 i 基因加入 j 基因的邻接列表
                }
            }
        }

        // 如果在基因库中没有找到 end 基因，返回 -1
        if (endIndex == -1) {
            return -1;
        }

        // 广度优先搜索（BFS）队列
        Queue<Integer> queue = new ArrayDeque<Integer>();
        boolean[] visited = new boolean[n];  // 标记基因是否已被访问过
        int step = 1;  // 步数，从 start 基因开始计数

        // 将与 start 基因相差一个字符的基因加入队列
        for (int i = 0; i < n; i++) {
            int mutations = 0;  // 记录 start 基因和 bank[i] 基因的差异数
            for (int k = 0; k < m; k++) {
                if (start.charAt(k) != bank[i].charAt(k)) {
                    mutations++;  // 如果字符不同，差异数加1
                }
                if (mutations > 1) {
                    break;  // 如果差异数超过1，跳出循环
                }
            }
            // 如果 start 和 bank[i] 只有一个字符差异，将 bank[i] 加入队列
            if (mutations == 1) {
                queue.offer(i);  // 将 bank[i] 的索引加入队列
                visited[i] = true;  // 标记 bank[i] 为已访问
            }
        }

        // 使用 BFS 进行最短路径查找
        while (!queue.isEmpty()) {
            int sz = queue.size();  // 当前队列中的元素数量（即当前层的节点数）
            // 遍历当前层的所有节点
            for (int i = 0; i < sz; i++) {
                int curr = queue.poll();  // 从队列中取出一个基因
                if (curr == endIndex) {
                    return step;  // 如果找到了 end 基因，返回当前的步数
                }
                // 遍历当前基因的所有邻接基因
                for (int next : adj[curr]) {
                    if (visited[next]) {
                        continue;  // 如果下一个基因已被访问过，跳过
                    }
                    visited[next] = true;  // 标记下一个基因为已访问
                    queue.offer(next);  // 将下一个基因加入队列
                }
            }
            step++;  // 完成一层遍历，步数加1
        }

        // 如果 BFS 完成后仍未找到 end 基因，返回 -1
        return -1;
    }
}

• 时间复杂度：$O(m \times n ^ 2)$
• 空间复杂度：$O(n ^ 2)$

不是很懂为什么方法二要给出一个时间复杂度更高的解法。

单词接龙

广度优先搜索

和上一题类似，把每个单词都抽象为一个点，如果两个单词可以只改变一个字母进行转换，那么说明他们之间有一条双向边。因此我们只需要把满足转换条件的点相连，就形成了一张图。基于该图，以 beginWord 为图的起点，以 endWord 为终点进行广度优先搜索，寻找 beginWord 到 endWord 的最短路径。

1. 先给每一个单词标号，即给每个单词分配一个 id。创建一个由单词 word 到 id 对应的映射 wordId，并将 beginWord 与 wordList 中所有的单词都加入这个映射中。之后我们检查 endWord 是否在该映射内，若不存在，则输入无解。我们可以使用哈希表实现上面的映射关系。
2. 枚举每一对单词的组合，判断它们是否恰好相差一个字符，以判断这两个单词对应的节点是否能够相连。但是这样效率太低，我们可以优化建图。

class Solution {
    // 定义单词到id映射和邻接表
    Map<String, Integer> word2id = new HashMap<>();
    List<List<Integer>> edge = new ArrayList<>();
    int nodeNum = 0;

    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        // 建立图
        for (String word : wordList) {
            addEdge(word);
        }
        // 起始节点加入图
        addEdge(beginWord);
        // 边界处理
        if (!word2id.containsKey(endWord)) {
            return 0;
        }
        // 定义距离数组，表示beginWord到当前节点的距离
        int[] dis = new int[nodeNum];
        Arrays.fill(dis, Integer.MAX_VALUE);
        // 起点终点索引
        int beginId = word2id.get(beginWord);
        int endId = word2id.get(endWord);
        dis[beginId] = 0;

        // 广度优先搜索
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(beginId);
        while (!queue.isEmpty()) {
            int x = queue.poll();
            if (x == endId) {
                return dis[x] / 2 + 1;
            }
            // 将所有相邻节点加入队列
            for (int it : edge.get(x)) {
                if (dis[it] == Integer.MAX_VALUE) {
                    dis[it] = dis[x] + 1;
                    queue.offer(it);
                }
            }
        }

        return 0;
    }

    // 建立边
    public void addEdge(String word) {
        // 加入映射
        addWord(word);
        // 获取id
        int id1 = word2id.get(word);
        char[] array = word.toCharArray();
        // 创建虚拟节点
        for (int i = 0; i < array.length; i++) {
            char tmp = array[i];
            array[i] = '*';
            String newWord = new String(array);
            addWord(newWord);
            // 添加边
            int id2 = word2id.get(newWord);
            edge.get(id1).add(id2);
            edge.get(id2).add(id1);
            // 还原
            array[i] = tmp;
        }
    }

    // 添加单词至映射
    public void addWord(String word) {
        if (!word2id.containsKey(word)) {
            word2id.put(word, nodeNum++);
            edge.add(new ArrayList<Integer>());
        }
    }
}

• 时间复杂度：$O(N \times C^2)$，其中 N 为 wordList 的长度，C 为列表中单词的长度。
• 空间复杂度：$O(N \times C^2)$。

双向广度优先搜索

一边从 beginWord 开始，另一边从 endWord 开始。我们每次从两边各扩展一层节点，当发现某一时刻两边都访问过同一顶点时就停止搜索。这就是双向广度优先搜索，它可以可观地减少搜索空间大小，从而提高代码运行效率。

class Solution {
    // 定义单词到id映射和邻接表
    Map<String, Integer> word2id = new HashMap<>();
    List<List<Integer>> edge = new ArrayList<>();
    int nodeNum = 0;

    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        // 建立图
        for (String word : wordList) {
            addEdge(word);
        }
        // 起始节点加入图
        addEdge(beginWord);
        // 边界处理
        if (!word2id.containsKey(endWord)) {
            return 0;
        }
        // 定义距离数组，表示beginWord到当前节点的距离
        int[] disBegin = new int[nodeNum];
        Arrays.fill(disBegin, Integer.MAX_VALUE);
        // 起点终点索引
        int beginId = word2id.get(beginWord);
        disBegin[beginId] = 0;
        Queue<Integer> queBegin = new LinkedList<>();
        queBegin.offer(beginId);

        // 定义距离数组，表示endWord到当前节点的距离
        int[] disEnd = new int[nodeNum];
        Arrays.fill(disEnd, Integer.MAX_VALUE);
        int endId = word2id.get(endWord);
        disEnd[endId] = 0;
        Queue<Integer> queEnd = new LinkedList<>();
        queEnd.offer(endId);

        // 广度优先搜索
        while (!queBegin.isEmpty() && !queEnd.isEmpty()) {
            // 从begin开始
            int queBeginSize = queBegin.size();
            for (int i = 0; i < queBeginSize; i++) {
                int nodeBegin = queBegin.poll();
                // 如果从后向前的搜索已经搜索过该节点
                if (disEnd[nodeBegin] != Integer.MAX_VALUE) {
                    return (disBegin[nodeBegin] + disEnd[nodeBegin]) / 2 + 1;
                }
                // 所有相邻节点加入队列
                for (int it : edge.get(nodeBegin)) {
                    if (disBegin[it] == Integer.MAX_VALUE) {
                        disBegin[it] = disBegin[nodeBegin] + 1;
                        queBegin.offer(it);
                    }
                }
            }

            // 从end开始
            int queEndSize = queEnd.size();
            for (int i = 0; i < queEndSize; i++) {
                int nodeEnd = queEnd.poll();
                // 如果从前向后已经搜索过该节点
                if (disBegin[nodeEnd] != Integer.MAX_VALUE) {
                    return (disBegin[nodeEnd] + disEnd[nodeEnd]) / 2 + 1;
                }
                // 所有相邻节点加入队列
                for (int it : edge.get(nodeEnd)) {
                    if (disEnd[it] == Integer.MAX_VALUE) {
                        disEnd[it] = disEnd[nodeEnd] + 1;
                        queEnd.offer(it);
                    }
                }
            }
        }

        return 0;
    }

    // 建立边
    public void addEdge(String word) {
        // 加入映射
        addWord(word);
        // 获取id
        int id1 = word2id.get(word);
        char[] array = word.toCharArray();
        // 创建虚拟节点
        for (int i = 0; i < array.length; i++) {
            char tmp = array[i];
            array[i] = '*';
            String newWord = new String(array);
            addWord(newWord);
            // 添加边
            int id2 = word2id.get(newWord);
            edge.get(id1).add(id2);
            edge.get(id2).add(id1);
            // 还原
            array[i] = tmp;
        }
    }

    // 添加单词至映射
    public void addWord(String word) {
        if (!word2id.containsKey(word)) {
            word2id.put(word, nodeNum++);
            edge.add(new ArrayList<Integer>());
        }
    }
}

• 时间复杂度：$O(N \times C^2)$
• 空间复杂度：$O(N \times C^2)$

总结

图的问题主要解决方法是深度优先搜索、广度优先搜索和并查集，以后要多加复习。