LeetCode 热题 100-堆
堆排序
建立一个大小为k的小根堆,遍历数组中的元素,如果有大于堆顶的,则替换堆顶并调整堆,最终堆顶就是第k个最大的元素。
- 小根堆操作:将以节点 i 为根的子树进行小根堆调整
- 获取左右子节点索引和当前节点索引
- 如果左子节点存在且小于当前节点,则更新最小节点索引;如果右子节点存在且小于当前节点或左子节点,则更新最小节点索引
- 如果最小节点索引不等于当前节点索引,则交换当前节点和最小节点,并继续调整最小堆。
- 建立小根堆: 从最后一个非叶子节点开始,依次向前调整节点,保证以每个节点为根的子树都是小根堆。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| class Solution {
public int findKthLargest(int[] nums, int k) {
int n = nums.length;
buildMinHeap(nums, k);
for (int i = k; i < n; i++) {
if (nums[i] > nums[0]) {
swap(nums, i, 0);
minHeapify(nums, 0, k);
}
}
return nums[0];
}
private void minHeapify(int[] nums, int index, int heapSize) {
int left = 2 * index + 1;
int right = 2 * index + 2;
int smallest = index;
if (left < heapSize && nums[left] < nums[smallest]) {
smallest = left;
}
if (right < heapSize && nums[right] < nums[smallest]) {
smallest = right;
}
if (smallest != index) {
swap(nums, index, smallest);
minHeapify(nums, smallest, heapSize);
}
}
private void buildMinHeap(int[] nums, int heapSize) {
for (int i = heapSize / 2; i >= 0; i--) {
minHeapify(nums, i, heapSize);
}
}
private void swap(int[] nums, int a, int b) {
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}
}
|
- 时间复杂度:O(nlong)
- 空间复杂度:O(logn)
快速排序
使用快速排序在每次调整时,都会确定一个元素的最终位置,且以该元素为界限,将数组分成了左右两个子数组,左子数组中的元素都比该元素小,右子树组中的元素都比该元素大。
这样,只要某次划分的元素恰好是第k个下标就找到了答案。并且我们只需关注第k个最大元素所在区间的排序情况,与第k个最大元素无关的区间排序都可以忽略。这样进一步减少了执行步骤。
- 分区函数:
- 选择左边界元素作为基准元素;
- 初始化左右指针;
- 开始分区:
- 从左往右找到第一个大于等于基准元素的元素;
- 从右往左找到第一个小于等于基准元素的元素;
- 如果左右指针相遇,则分区完成,退出循环;
- 交换不符合条件的元素;
- 分区完成,将基准元素放置在正确的位置上;
- 返回基准元素的位置。
- 快速选择:
- 分区并获取基准元素的位置;
- 将 k 转换为目标数组下标;
- 如果基准元素的位置就是目标位置,则返回该元素;
- 如果基准元素的位置小于目标位置,则在右侧继续查找;
- 如果基准元素的位置大于目标位置,则在左侧继续查找。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
public int findKthLargest(int[] nums, int k) {
return quickSelect(nums, 0, nums.length - 1, k);
}
private int quickSelect(int[] nums, int left, int right, int k) {
int pivotIndex = partion(nums, left, right);
int target = nums.length - k;
if (pivotIndex == target) {
return nums[pivotIndex];
} else if (pivotIndex < target) {
return quickSelect(nums, pivotIndex + 1, right, k);
} else {
return quickSelect(nums, left, pivotIndex - 1, k);
}
}
private int partion(int[] nums, int left, int right) {
int pivot = nums[left];
int i = left, j = right + 1;
while (i < j) {
while(++i < right && nums[i] < pivot);
while(--j > left && nums[j] > pivot);
if (i >= j) {
break;
}
swap(nums, i, j);
}
swap(nums, left, j);
return j;
}
private void swap(int[] nums, int a, int b) {
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}
}
|
- 时间复杂度:O(nlogn)
- 空间复杂度:O(logn)
对于快排左右指针初始化及边界判断问题需要再好好想想。
堆
用哈希表存储统计的元素及其个数,然后按照其个数大小进行排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public int[] topKFrequent(int[] nums, int k) {
HashMap<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
if (map.containsKey(num)) {
map.put(num, map.get(num) + 1);
} else{
map.put(num, 1);
}
}
PriorityQueue<Integer> heap = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer a, Integer b) {
return map.get(a) - map.get(b);
}
});
for (Integer key : map.keySet()) {
if (heap.size() < k) {
heap.add(key);
} else if (map.get(key) > map.get(heap.peek())) {
heap.remove();
heap.add(key);
}
}
int[] res = new int[k];
int i = 0;
while (!heap.isEmpty()) {
res[i++] = heap.remove();
}
return res;
}
}
|
- 时间复杂度:O(nlogk)
- 空间复杂度:O(n)
桶排序
使用哈希表统计频率,统计完成后,创建一个数组,将频率作为数组下标,对于出现频率不同的数字集合,存入对应的数组下标即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public int[] topKFrequent(int[] nums, int k) {
HashMap<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
if (map.containsKey(num)) {
map.put(num, map.get(num) + 1);
} else{
map.put(num, 1);
}
}
List<Integer>[] list = new List[nums.length + 1];
for (int key : map.keySet()) {
int i = map.get(key);
if (list[i] == null) {
list[i] = new ArrayList();
}
list[i].add(key);
}
List<Integer> res = new ArrayList();
for (int i = list.length - 1; i >= 0 && res.size() < k; i--) {
if (list[i] != null) {
res.addAll(list[i]);
}
}
return res.stream().mapToInt(Integer::intValue).toArray();
}
}
|
随着 addNum 不断地添加数字,我们需要:
- 保证 left 的大小和 right 的大小尽量相等。规定:在有奇数个数时,left 比 right 多 1 个数。
- 保证 left 的所有元素都小于等于 right 的所有元素。
只要时时刻刻满足以上两个要求(满足中位数的定义),我们就可以用 left 中的最大值以及 right 中的最小值计算中位数。
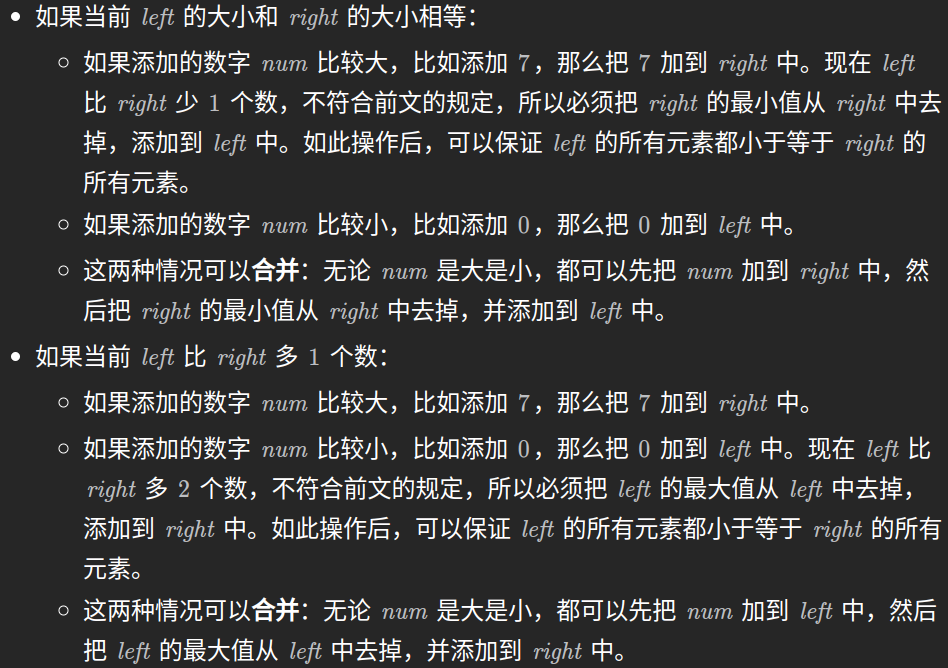
即left是最大堆,right时最小堆。如果当前有奇数个元素,中位数是 left 的堆顶。如果当前有偶数个元素,中位数是 left 的堆顶和 right 的堆顶的平均值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class MedianFinder {
private final PriorityQueue<Integer> left = new PriorityQueue<>((a,b) -> b - a);
private final PriorityQueue<Integer> right = new PriorityQueue<>();
public MedianFinder() {
}
public void addNum(int num) {
if (left.size() == right.size()) {
right.offer(num);
left.offer(right.poll());
}
else {
left.offer(num);
right.offer(left.poll());
}
}
public double findMedian() {
if (left.size() > right.size()) {
return left.peek();
}
return (left.peek() + right.peek()) / 2.0;
}
}
|
- 时间复杂度:O(logq),添加数字。
- 空间复杂度:O(q)
不得不再次感叹灵神的思路太通透了!
总结
对于堆,可以自己用数组模拟实现,也可以使用PriorityQueue。对于java中的各种数据结构还非常不熟悉,要一边刷题一边复习数据结构的使用。
