LeetCode 热题 100-二分查找

搜索插入位置

闭区间

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n - 1;
        while (left <= right) {
            int mid = (left + right) >> 1;
            if (nums[mid] < target) {
                left = mid + 1;
            } else{
                right = mid - 1;
            }
        }
        return left;
    }
}

左闭右开

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n;
        while (left < right) {
            int mid = (left + right) >> 1;
            if (nums[mid] < target) {
                left = mid + 1;
            } else{
                right = mid;
            }
        }
        return left;
    }
}

开区间

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int left = -1, right = n;
        while (left + 1 < right) {
            int mid = (left + right) >> 1;
            if (nums[mid] < target) {
                left = mid;
            } else{
                right = mid;
            }
        }
        return right;
    }
}

时间复杂度：O(logn)
空间复杂度：O(1)

搜索二维矩阵

z字形查找

从矩阵的右上角开始搜索，大于目标则列坐标-1，小于目标则行坐标+1.

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        int row = 0, col = n - 1;
        while (true) {
            if (matrix[row][col] == target) {
                return true;
            } else if (matrix[row][col] < target) {
                row++;
            } else{
                col--;
            }
            if (row >= m || col < 0) {
                break;
            }
        }
        return false;
    }
}

时间复杂度：O(m + n)
空间复杂度：O(1)

二分查找

将二维数组看成一维数组，实现时只需将 a[i] 转换成矩阵中的行号和列号。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        int left = 0, right = m * n;
        // 左闭右开
        while (left < right) {
            int mid = (left + right) >> 1;
            int x = matrix[mid / n][mid % n];   // 转换成行号和列号
            if (x == target) {
                return true;
            } else if (x < target) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return false;
    }
};

时间复杂度：O(log(mn))
空间复杂度：O(1)

在排序数组中查找元素的第一个和最后一个位置

二分查找

其实就是lower_bound和upper_bound实现的功能，找到第一个大于等于目标的元素和第一个大于目标的元素下标。

实现lower_bound函数，右边界不断向左收缩，无需再重新实现查找右边界的函数，直接调用lower_bound，目标值设为target+1即可找到（左闭右开，最终右边界值-1）。

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int n = nums.length;
        int start = lowerBound(nums, target);
        // 边界处理
        if (start == n || nums[start] != target) {
            return new int[]{-1, -1};
        }
        int end = lowerBound(nums, target + 1) - 1;
        return new int[]{start, end};
    }

    private int lowerBound(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] >= target) {
                right = mid - 1;    // 向左收缩边界
            } else {
                left = mid + 1;
            }
        }

        return left;
    }
}

时间复杂度：O(logn)
空间复杂度：O(1)

搜索旋转排序数组

二分查找

判断哪一部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界：

如果 [left, mid - 1] 是有序数组，即nums[left] <= nums[mid]：如果target >= nums[left] && target < nums[mid]，则在左半部分，否则在右半部分；
否则如果nums[left] > nums[mid]，则右半部分有序：如果target > nums[mid] && target <= nums[right]，则在右半部分，否则在左半部分。

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                return mid;
            }
            // 左半部分有序
            if (nums[left] <= nums[mid]) {
                // 在左半部分
                if (target >= nums[left] && target < nums[mid]) {
                    right = mid - 1;
                } else {
                    left = mid + 1;
                }
            } else {
                // 在右半部分
                if (target > nums[mid] && target <= nums[right]) {
                    left = mid + 1;
                } else {
                    right = mid - 1;
                }
            }
        }
        return -1;
    }
}

时间复杂度：O(logn)
空间复杂度：O(1)

寻找旋转排序数组中的最小值

二分查找

数组经过「旋转」之后，会有两种情况，第一种就是原先的升序序列，另一种是两段升序的序列。第一种的最小值在最左边。第二种最小值在第二段升序序列的第一个元素。

二分法：left和right分别指向数组首尾。计算mid:

如果nums[mid] > nums[right]，则最小值一定在mid右侧；
否则一定在mid或者mid的左侧。

class Solution {
    public int findMin(int[] nums) {
        int n = nums.length;
        int left = 0, right = n - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > nums[right]) {
                left = mid + 1;
            } else{
                right = mid;
            }
        }

        return nums[left];
    }
}

时间复杂度：O(logn)
空间复杂度：O(1)

寻找两个正序数组的中位数

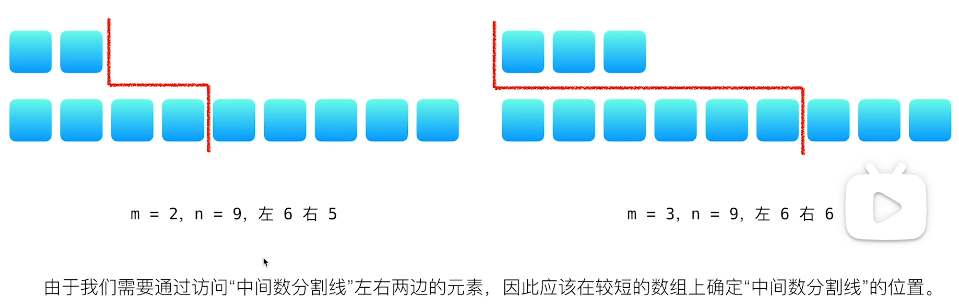
二分查找

中位数把数组分割成了左右两部分，并且左右两部分元素个数相等。如果两个数组元素个数为偶数，单侧元素个数为$(n1+n2) / 2$个；否则是$(n1+n2)/2 + 1$个，可以总结为单侧元素个数： $\lfloor \frac{(n1 + n2 + 1)}{2} \rfloor$ 。现在的问题就变为了：如何在两个有序数组中找到前 k 小的元素位置？

Alt text

确保 nums1 是较小的数组：我们总是对较短的数组进行二分查找，减少搜索空间。
二分查找：在较短数组中查找一个合适的分割点，使得两数组的左半部分和右半部分满足合并后的中位数条件。
计算中位数：
- 如果数组的总长度为奇数，中位数是左半部分的最大值。
- 如果数组的总长度为偶数，中位数是左半部分最大值与右半部分最小值的平均值。

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        // 确保nums1是较小的数组
        if (m > n) {
            return findMedianSortedArrays(nums2, nums1);
        }
        int k = (m + n + 1) / 2;
        // 双指针
        int left = 0, right = m;
        while (left <= right) {
            int partition1 = left + (right - left) / 2; // 第一个数组的分割点
            int partition2 = k - partition1;
            // 获取边界值
            int leftMax1 = partition1 == 0 ? Integer.MIN_VALUE : nums1[partition1 - 1];
            int rightMin1 = partition1 == m ? Integer.MAX_VALUE : nums1[partition1];
            int leftMax2 = partition2 == 0 ? Integer.MIN_VALUE : nums2[partition2 - 1];
            int rightMin2 = partition2 == n ? Integer.MAX_VALUE : nums2[partition2];

            if (leftMax1 <= rightMin2 && leftMax2 <= rightMin1) {
                if ((m + n) % 2 == 0) {
                    return (Math.max(leftMax1, leftMax2) + Math.min(rightMin1, rightMin2)) / 2.0;
                } else {
                    return Math.max(leftMax1, leftMax2);
                }
            } else if (leftMax1 > rightMin2) { // 第一个数组左边元素太多了
                right = partition1 - 1;
            } else {  // 第一个分组右边元素太多了
                left = partition1 + 1;
            }
        }
        throw new IllegalArgumentException("Input arrays are not sorted.");
    }
}

时间复杂度：O(log(m + n))
空间复杂度：O(1)

总结

二分查找的部分要注意初始化left和right时是定义区间为左开右闭还是闭区间，两种定义的循环判断条件是不同的。最后一道题有些难，要经常复习。

算法笔记 > 二分查找

#leetcode-hot100

LeetCode 热题 100-二分查找

http://example.com/2024/12/13/posts/hot100-11/

作者

Xuan Yang

发布于

2024年12月13日

许可协议

LeetCode 热题 100-栈上一篇

LeetCode 热题 100-回溯法下一篇