LeetCode 热题 100-二叉树

LeetCode 热题 100-二叉树

二叉树的中序遍历

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        dfs(root, ans);
        return ans;
    }
    void dfs(TreeNode* root, vector<int>& ans){
        if(!root){
            return;
        }
        dfs(root->left, ans);
        ans.push_back(root->val);
        dfs(root->right, ans);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)，空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。

迭代

采用迭代写法，需要借助栈结构来实现：

  • 前序遍历；出栈顺序：根-左-右；入栈顺序：右-左-根；
  • 中序遍历；出栈顺序：左-根-右；入栈顺序：右-根-左；
  • 后序遍历；出栈顺序：左-右-根；入栈顺序：根-右-左；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        stack<TreeNode*> stk;
        while(root || !stk.empty()){
            // 不断把左子树压入栈
            while(root){
                stk.push(root);
                root = root->left;
            }
            // 出栈，遍历
            root = stk.top();
            stk.pop();
            ans.push_back(root->val);
            root = root->right;
        }

        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

Morris遍历

  1. 若 cur == null，则过程停止，否则继续下面的过程；
  2. 若 cur 无左子树，则访问当前元素，并令 cur = cur.right；
  3. 若 cur 有左子树，则找到 cur 左子树上最右的节点，记作 mostRight：
    • 若 mostRight.right == null，则令 mostRight.right = cur，即让 mostRight 的 right 指针指向当前节点 cur，然后令 cur = cur.left；
    • 若 mostRight.right == cur， 说明我们已经遍历完的左子树，则访问当前元素，并令 mostRight.right = null，即让 mostRight 的 right 指针指向空，然后令 cur = cur.right。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        while(root){
            // 左子树为空，遍历该节点，并继续遍历右子树
            if(root->left == nullptr){
                ans.push_back(root->val);
                root = root->right;
            }else{
                // 找到最右边的节点
                TreeNode* predecessor = root->left;
                while(predecessor->right && predecessor->right != root){
                    predecessor = predecessor->right;
                }
                // 如果它的右指针为空，则指向root，继续遍历左子树
                if(predecessor->right == nullptr){
                    predecessor->right = root;
                    root = root->left;
                }else{
                    // 左子树已经遍历完，断开链接
                    ans.push_back(root->val);
                    predecessor->right = nullptr;
                    root = root->right;
                }
            }
        }
        return ans;
    }
};
  • 时间复杂度：O(n)，每个节点会被访问两次。
  • 空间复杂度：O(1)

二叉树的最大深度

递归

当前节点为空则返回0，否则递归计算左右子树最大深度，取较大值，再+1.

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr){
            return 0;
        }
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)，此时树为一条链。

迭代

广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候，不同于广度优先搜索的每次只从队列里拿出一个节点，我们需要将队列里的所有节点都拿出来进行拓展，这样能保证每次拓展完的时候队列里存放的是当前层的所有节点，即我们是一层一层地进行拓展，最后我们用一个变量 ans 来维护拓展的次数，该二叉树的最大深度即为 ans。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int maxDepth(TreeNode* root) {
        // 处理边界
        if(root == nullptr){
            return 0;
        }
        queue<TreeNode*> que;
        int ans = 0;
        que.push(root);
        while(!que.empty()){
            // 对当前层进行扩展
            int size = que.size();
            for(int i = 0; i < size; i++){
                TreeNode* node = que.front();
                que.pop();
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            ans += 1;
        }
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)，队列消耗的空间。

翻转二叉树

递归

root为空，则无需交换，直接返回。否则递归交换左右子树，然后再将左右子树交换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        // 处理边界
        if(root == nullptr){
            return root;
        }
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);
        root->left = right;
        root->right = left;

        return root;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)，最坏情况下，树形成链状，空间复杂度为 O(N)。

[!NOTE]
之后再练练几种遍历的迭代和Morris写法。

对称二叉树

递归

检查左右子树是否相等:

  • 左右子树有一个为空，不相等；都为空，相等。
  • 检查左右子树值以及左子树的右子树和右子树的左子树是否相等，以及左子树的左子树和右子树的右子树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return isSameTree(root->left, root->right);
    }

    bool isSameTree(TreeNode* leftTree, TreeNode* rightTree){
        if(leftTree == nullptr || rightTree == nullptr){
            return leftTree == rightTree;
        }
        return leftTree->val == rightTree->val && isSameTree(leftTree->right, rightTree->left) && isSameTree(leftTree->left, rightTree->right);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

迭代

用广度优先搜索的方法，如果当前左子树不等于右子树，直接返回false，否则按照左子树的左子树、右子树的右子树、左子树的右子树、右子树的左子树的顺序加入队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        queue<TreeNode*> que;
        que.push(root->left);
        que.push(root->right);

        while(!que.empty()){
            TreeNode* leftTree = que.front();
            que.pop();
            TreeNode* rightTree = que.front();
            que.pop();
            if(leftTree == nullptr && rightTree == nullptr) continue;
            if(leftTree == nullptr || rightTree == nullptr || leftTree->val != rightTree->val){
                return false;
            }

            que.push(leftTree->left);
            que.push(rightTree->right);
            que.push(leftTree->right);
            que.push(rightTree->left);
        }

        return true;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

二叉树的直径

深度优先搜索

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

经过一个节点的最长路径应该等于它左子树的最大深度+右子树最大深度.即，dfs返回的是最大深度而不是直径，最大深度等于左子树深度和右子树深度的较大值+1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int ans = 0;
    int diameterOfBinaryTree(TreeNode* root) {
        dfs(root);
        return ans;
    }

    int dfs(TreeNode* root){
        if(root == nullptr){
            return 0;
        }
        int maxLeft = dfs(root->left);
        int maxRight = dfs(root->right);
        ans = max(ans, maxLeft + maxRight);

        return max(maxLeft, maxRight) + 1;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

二叉树的层序遍历

广度优先搜索

可以当做层序遍历的模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        if(root == nullptr){
            return ans;
        }
        queue<TreeNode*> que;
        que.push(root);

        while(!que.empty()){
            int size = que.size();
            vector<int> cur;
            for(int i = 0; i < size; i++){
                TreeNode* node = que.front();
                que.pop();
                cur.push_back(node->val);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            ans.push_back(cur);
        }

        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

将有序数组转换为二叉搜索树

分治法

将中点作为根节点，中点左侧作为左子树，右侧作为右子树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return dfs(nums, 0, nums.size());
    }

    TreeNode* dfs(vector<int>& nums, int left, int right){
        if(left == right){
            return nullptr;
        }
        int mid = (left + right) >> 1;
        return new TreeNode(nums[mid], dfs(nums, left, mid), dfs(nums, mid+1, right));
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(logn)

验证二叉搜索树

递归

对于一棵二叉树，如果其左子树不为空且节点值小于根节点，并且其右子树不为空且节点值大于根节点，递归左右子树也都满足，则是二叉搜索树。逻辑错误！只检查了当前节点与它的左右子节点的关系（根节点与直接左右子节点之间的比较），但对于整个树的有效性来说，还需要确保每个子树的节点都满足二叉搜索树的性质，也就是说子树的节点值必须大于它的左子树所有节点的值，且小于它的右子树所有节点的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return helper(root, LONG_MIN, LONG_MAX);
    }

    bool helper(TreeNode* root, long long lower, long long upper){
        if(root == nullptr){
            return true;
        }
        if(root->val <= lower || root->val >= upper){
            return false;
        }
        return helper(root->left, lower, root->val) && helper(root->right, root->val, upper);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

中序遍历

在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值。如果均大于说明这个序列是升序的，整棵树是二叉搜索树，否则不是。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        // 迭代实现中序遍历
        stack<TreeNode*> stk;
        long long inorder = LONG_MIN;

        while(!stk.empty() || root != nullptr){
            while(root != nullptr){
                stk.push(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            // 判断中序遍历的当前节点值是否满足条件
            if(root->val <= inorder){
                return false;
            }
            inorder = root->val;
            root = root->right;
        }
        return true;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

二叉搜索树中第k小的元素

中序遍历

考虑中序遍历，用一个变量来计数，遍历到的第k个元素就是第k小的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        stack<TreeNode*> stk;
        int cnt = 0;
        while(!stk.empty() || root != nullptr){
            while(root != nullptr){
                stk.push(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            // 更新变量
            cnt++;
            if(cnt == k){
                return root->val;
            }
            root = root->right;
        }
        return -1;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

平衡二叉搜索树具有如下性质：

  • 平衡二叉搜索树中每个结点的左子树和右子树的高度最多相差 1；
  • 平衡二叉搜索树的子树也是平衡二叉搜索树；
  • 一棵存有 n 个结点的平衡二叉搜索树的高度是 O(logn)。

晚上再看二叉平衡树的做法。

将二叉搜索树变平衡

二叉树的右视图

深度优先搜索

先递归右子树，再递归左子树，当某个深度首次到达时，对应的节点就在右视图中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> ans;

    vector<int> rightSideView(TreeNode* root) {
        dfs(root, 0);
        return ans;
    }

    void dfs(TreeNode* root, int depth){
        if(root == nullptr){
            return;
        }
        // 某个深度首次达到
        if(depth == ans.size()){
            ans.push_back(root->val);
        }
        // 先递归右子树，保证首次遇到的是最右边的节点
        dfs(root->right, depth + 1);
        dfs(root->left, depth + 1);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

广度优先搜索

用层序遍历的方法，但在每次放入队列节点时，先放入右子树节点，这样对每一层遍历时，取出的第一个节点就是最右边的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> ans;
        if(root == nullptr){
            return ans;
        }
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            int size = que.size();
            for(int i = 0; i < size; i++){
                TreeNode* node = que.front();
                que.pop();
                if(i == 0){
                    ans.push_back(node->val);
                }
                if(node->right) que.push(node->right);
                if(node->left) que.push(node->left);
            }
        }
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

二叉树展开为链表

先序遍历

很容易按照先序遍历的顺序链接成链表。用一个数组存放先序遍历的节点指针，然后对每一个节点，将其左子树置空，将其右子树置为下一个节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    void flatten(TreeNode* root) {
        vector<TreeNode*> vec;
        stack<TreeNode*> stk;
        TreeNode* node = root;
        while(!stk.empty() || node){
            while(node){
                vec.push_back(node);    // 先序遍历
                stk.push(node);
                node = node->left;
            }
            node = stk.top();
            stk.pop();
            node = node->right;
        }

        for(int i = 1; i < vec.size(); i++){
            vec[i-1]->left = nullptr;
            vec[i-1]->right = vec[i];
        }
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

头插法

按照右子树 - 左子树 - 根的顺序 DFS 这棵树。DFS 的同时，记录当前链表的头节点为 head。一开始 head 是空节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    TreeNode* head;

    void flatten(TreeNode* root) {
        if(root == nullptr){
            return;
        }

        // 递归右子树、左子树
        flatten(root->right);
        flatten(root->left);
        // 头插法
        root->left = nullptr;
        root->right = head;
        head = root;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

寻找前驱节点

对于当前节点，如果其左子节点不为空，则在其左子树中找到最右边的节点，作为前驱节点，将当前节点的右子节点赋给前驱节点的右子节点，然后将当前节点的左子节点赋给当前节点的右子节点，并将当前节点的左子节点设为空。对当前节点处理结束后，继续处理链表中的下一个节点，直到所有节点都处理结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode* cur = root;
        while(cur){
            if(cur->left){
                TreeNode* next = cur->left;
                // 找到最右边的节点
                TreeNode* pre = next;
                while(pre->right){
                    pre = pre->right;
                }
                // 当前节点右子树赋给前驱节点右子树
                pre->right = cur->right;
                cur->left = nullptr;
                cur->right = next;
            }
            cur = cur->right;
        }
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

从前序与中序遍历序列构造二叉树

递归

利用递归和分治策略，通过遍历数组的信息来确定二叉树的结构。用哈希表预处理中序遍历的数组，这样之后可以在O(1)的时间内找到它。从 Preorder 中可以直接确定子树的根节点，而通过 Inorder 可以确定根节点在整棵树中的位置，从而区分左子树和右子树的范围。

二叉树的根节点是 Preorder 的第一个元素。在 Inorder 中找到根节点的位置：

该位置的左侧为左子树的元素。
该位置的右侧为右子树的元素。

根据子树的大小（Inorder 左侧元素个数）确定 Preorder 中对应的子树范围，递归处理。当当前的子树范围为空时，返回空指针。

总结为：

  1. 确定根节点
  2. 划分左右子树
  3. 构建左右子树
  4. 连接子树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        // 哈希表预处理中序数组
        unordered_map<int, int> hash;
        for(int i = 0; i < n; i++){
            hash[inorder[i]] = i;
        }

        // 定义递归函数处理
        function<TreeNode*(int, int, int, int)> dfs = [&] (int preLeft, int preRight, int inLeft, int inRight) -> TreeNode* {
            // 递归结束
            if(preLeft == preRight){
                return nullptr;
            }
             // O(1)时间在中序遍历中找到根节点
            int leftSize = hash[preorder[preLeft]] - inLeft;
            // 递归遍历左右子树
            TreeNode* leftTree = dfs(preLeft+1, preLeft+1+leftSize, inLeft, inLeft+leftSize);
            TreeNode* rightTree = dfs(preLeft+1+leftSize, preRight, inLeft+leftSize+1, inRight);
            // 连接子树
            return new TreeNode(preorder[preLeft], leftTree, rightTree);
        };

        return dfs(0, n, 0, n);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

迭代

  • 用一个栈和一个指针辅助进行二叉树的构造。初始时栈中存放了根节点（前序遍历的第一个节点），指针指向中序遍历的第一个节点；
  • 依次枚举前序遍历中除了第一个节点以外的每个节点。如果 index 恰好指向栈顶节点，那么我们不断地弹出栈顶节点并向右移动 index，并将当前节点作为最后一个弹出的节点的右儿子；如果 index 和栈顶节点不同，我们将当前节点作为栈顶节点的左儿子；
  • 无论是哪一种情况，我们最后都将当前的节点入栈。

看不太明白……

路径总和III

暴力

  1. 定义 rootSum(p,val) 表示以节点 p 为起点向下且满足路径总和为 val 的路径数目。对二叉树上每个节点 p 求出 rootSum(p,targetSum)，然后对这些路径数目求和即为返回结果。
  2. 对节点 p 求 rootSum(p,targetSum) 时，以当前节点 p 为目标路径的起点递归向下进行搜索。对左子树和右子树进行递归搜索。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int pathSum(TreeNode* root, int targetSum) {
        if(!root){
            return 0;
        }
        // 对每一个节点都要遍历
        int ans = rootSum(root, targetSum);
        // 不包含当前节点
        ans += pathSum(root->left, targetSum);
        ans += pathSum(root->right, targetSum);

        return ans;
    }

    int rootSum(TreeNode* root, int targetSum){
        if(!root){
            return 0;
        }

        int res = 0;
        if(root->val == targetSum){
            res++;
        }

        res += rootSum(root->left, targetSum - root->val);
        res += rootSum(root->right, targetSum - root->val);

        return res;
    }
};
  • 时间复杂度：$O(n^2)$
  • 空间复杂度：O(n)，递归栈空间。

前缀和

  1. 遍历每个节点，更新当前路径的前缀和。
  2. 检查哈希表中是否存在满足条件的前缀和，如果存在，累加路径数。注意哈希表初始时应把0加入，要想把任意路径和都表示成两个前缀和的差，必须添加一个 0，否则当路径是前缀时（从根节点开始的路径），没法减去一个数。
  3. 递归左右子树。
  4. 回溯时移除当前节点路径和，恢复状态。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int pathSum(TreeNode* root, int targetSum) {
        int ans = 0;
        unordered_map<long long, int> cnt{{0, 1}};

        function<void(TreeNode*, long long)> dfs = [&] (TreeNode* node, long long sum) {
            // 递归结束
            if(node == nullptr){
                return;
            }
            sum += node->val;
            // 查找是否存在
            ans += cnt.contains(sum - targetSum) ? cnt[sum - targetSum] : 0;
            cnt[sum]++;
            // 递归左右子树
            dfs(node->left, sum);
            dfs(node->right, sum);
            // 还原
            cnt[sum]--;
        };
        dfs(root, 0);
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

二叉树的最近公共祖先

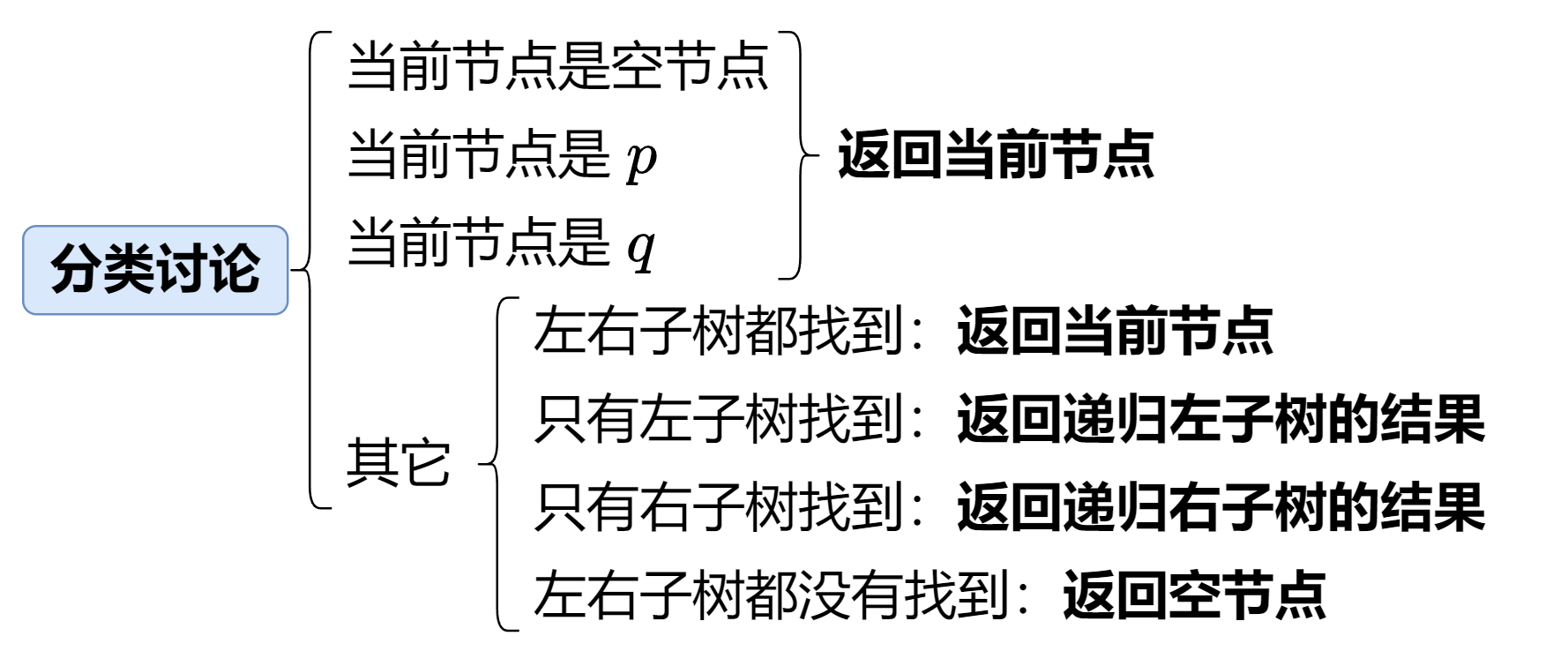
递归

Alt text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 返回当前节点
        if(root == NULL || root == p || root == q){
            return root;
        }
        // 在左右子树中查找
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);

        // 左右都找到了，则说明当前节点是最近公共祖先
        if(left && right){
            return root;
        }

        // 否则返回一棵子树的结果
        return left ? left : right;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

二叉树中的最大路径和

递归

如果当前节点为空，返回0.定义函数dfs用于计算从某个节点到叶子节点的路径和，它等于左子树最大路径和和右子树最大路径和的较大值再+1.函数内部更新全局最大路径和，当前路径和等于左子树最大路径和+右子树最大路径和+当前节点值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int ans = INT_MIN;
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return ans;
    }

    int dfs(TreeNode* root){
        // 递归结束
        if(root == nullptr){
            return 0;
        }

        // 递归计算左右子树
        int left = max(dfs(root->left), 0);
        int right = max(dfs(root->right), 0);
        // 更新答案
        ans = max(ans, left + right + root->val);

        return max(left, right) + root->val;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

总结

二叉树部分的题目之前大部分都做过，但是在思考递归时还是有些混乱，要经常复习。遗留问题：二叉平衡树，二叉树的迭代+Morris遍历。

算法笔记 > 二叉树
#leetcode-hot100
LeetCode 热题 100-二叉树
http://example.com/2024/12/04/posts/hot100-8/
作者
Xuan Yang
发布于
2024年12月4日
许可协议