LeetCode 热题 100-链表 双指针
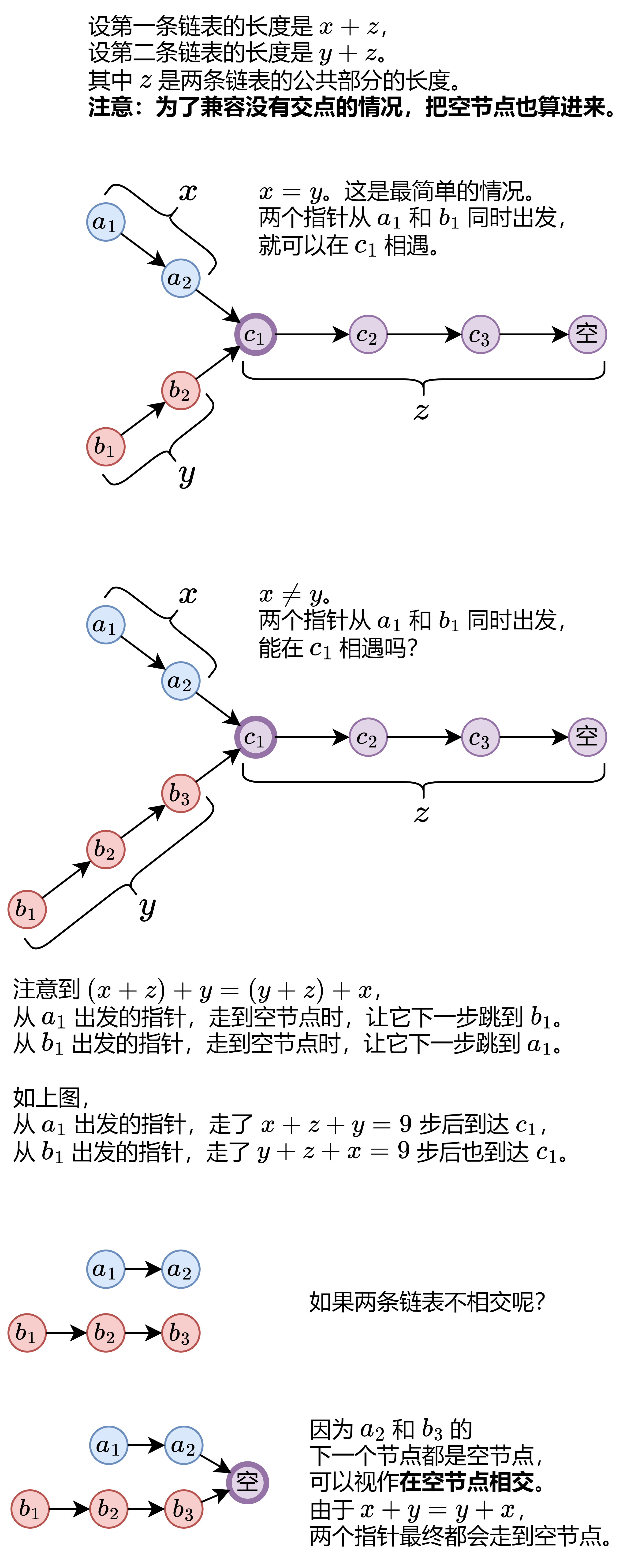
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution {public :ListNode *getIntersectionNode (ListNode *headA, ListNode *headB) {while (p != q){return p;
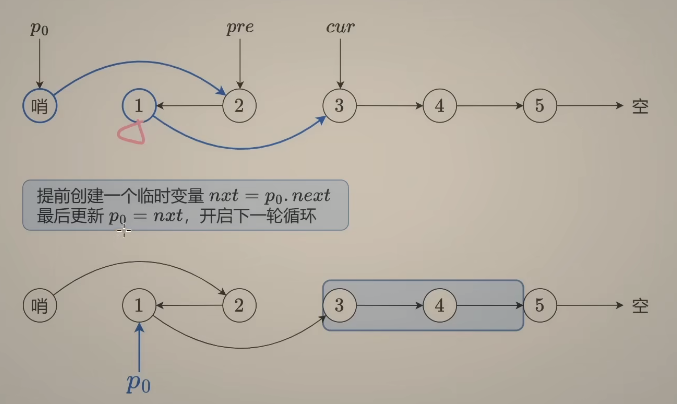
迭代 在遍历链表时,将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点,因此必须事先存储其前一个节点。在更改引用之前,还需要存储后一个节点。最后返回新的头引用。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution {public :ListNode* reverseList (ListNode* head) {nullptr ;while (cur){return pre;
递归 如果当前链表为空,或者只剩下一个未反转,直接返回head。否则,先递归反转后续的所有节点,得到反转后的头,就是该链表新的头。再将当前节点next的next指向当前节点,注意将当前节点的next置空。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public :ListNode* reverseList (ListNode* head) {if (!head || !head->next){return head;reverseList (head->next);nullptr ;return newHead;
分析 先将链表从中间分开,然后反转后半部分链表,再一一比较两个链表的节点。从中间分开可以用快慢指针,即慢指针走一步,快指针走两步,当快指针走到最后时,慢指针刚好指向中间。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class Solution {public :bool isPalindrome (ListNode* head) while (fast && fast->next){if (fast){reverseList (mid);while (half){if (head->val != half->val){return false ;return true ;ListNode* reverseList (ListNode* head) {nullptr ;while (cur){return pre;
分析 和上题思路一样,找到中点,将后半部分反转,注意将中间断开,然后按照归并排序合并的方法重组链表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 class Solution {public :void reorderList (ListNode* head) findMid (head);reverseList (mid);while (half->next){ListNode* findMid (ListNode* head) {while (fast && fast->next){return slow;ListNode* reverseList (ListNode* head) {nullptr ;while (cur){return pre;
快慢指针 定义快慢指针,如果两指针能够相遇,则说明存在环。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public :bool hasCycle (ListNode *head) while (fast && fast->next){if (slow == fast){return true ;return false ;
快慢指针 假设入环点距链表头为a,相遇点距入环点为b,相遇点到最后是c,则有a + n(b + c) = 2(a + b),得到a = c + (n-1)(b+c),即从链表头到入环点的距离等于从相遇点出发走了n-1次环的距离,即如果定义一个指针从链表头出发,一个指针从相遇点出发,每次都向后走一步,他们最终会相遇,相遇的地点就是入环点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution {public :ListNode *detectCycle (ListNode *head) {while (fast && fast->next){if (slow == fast){while (ptr != slow){return ptr;return NULL ;
时间复杂度:O(n),在最初判断快慢指针是否相遇时,slow 指针走过的距离不会超过链表的总长度;随后寻找入环点时,走过的距离也不会超过链表的总长度。
空间复杂度:O(1)
归并排序 不断比较两链表的节点值,将较小的节点加入新链表,继续向后遍历。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Solution {public :ListNode* mergeTwoLists (ListNode* list1, ListNode* list2) {new ListNode ();while (list1 && list2){if (list1->val < list2->val){else {while (list1){while (list2){return dummy->next;
模拟 模拟从个位加到最高位即可,注意维护进位标志,如果最后的进位是1,还需要再加一个新节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 class Solution {public :ListNode* addTwoNumbers (ListNode* l1, ListNode* l2) {new ListNode ();int carry = 0 ;while (l1 && l2){int sum = l1->val + l2->val + carry;10 ;new ListNode (sum % 10 );while (l1){int sum = l1->val + carry;10 ;new ListNode (sum % 10 );while (l2){int sum = l2->val + carry;10 ;new ListNode (sum % 10 );if (carry){new ListNode (carry);return dummy->next;
时间复杂度:O(n),n为两链表长度的较大值。
空间复杂度:O(1),不计入返回结果的空间复杂度。
快慢指针 最简单的方法是遍历一遍链表,得到链表的长度,然后从头走len-n步即找到倒数第n个节点。考虑只遍历一次链表:让一个指针先走n步,然后两指针同时走,当先走的指针走到空时,即它又走了len-n步,那么从头出发的指针也走了len-n步,它所指向的就是倒数第n个结点。这样能够找到要删除的节点,但是要删除节点,应该找到它的前一个节点。为了方便处理删除头结点的情况,定义一个哑节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public :ListNode* removeNthFromEnd (ListNode* head, int n) {new ListNode ();for (int i = 0 ; i < n; i++){while (fast->next){return dummy->next;
如果要delete这个结点,可以先将它保存,再delete掉。
迭代 定义哑节点方便操作,作为pre,定义当前指针left和下一个指针right,同时保存再下一个指针next,先让pre->next指向right,right->next指向left,left->next指向next。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public :ListNode* swapPairs (ListNode* head) {new ListNode ();while (left && left->next){return dummy->next;
递归 递归结束:head为空或者head->next为空,返回head。
否则,先交换后面的链表,即递归调用swapPairs(head->next->next),然后将head->next指向返回的链表头,而原来的next指向head,再返回next。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution {public :ListNode* swapPairs (ListNode* head) {if (!head || !head->next){return head;swapPairs (head->next->next);return newHead;
分析 首先统计链表节点个数,然后k 个一组处理,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 class Solution {public :ListNode* reverseKGroup (ListNode* head, int k) {int n = 0 ;while (cur){new ListNode (0 , head);nullptr ;for (; n >= k; n-= k){for (int i = 0 ; i < k; i++){return dummy->next;
回溯+哈希表 定义一个哈希表,用于存储节点的副本,如果这个节点已经存在,就直接返回,如果不存在,就复制一份,然后递归复制它的next和random。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public :Node* copyRandomList (Node* head) {if (head == NULL ){return head;if (!cache.count (head)){new Node (head->val);copyRandomList (head->next);copyRandomList (head->random);return cache[head];
时间复杂度:O(n),其中 n 是链表的长度。对于每个节点,我们至多访问其「后继节点」和「随机指针指向的节点」各一次,均摊每个点至多被访问两次。
空间复杂度:O(n),哈希表空间开销。
迭代+节点拆分
把每个节点复制一份链接在原节点的后边。
复制节点的random就是原节点的random的next。
分离链表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 class Solution {public :Node* copyRandomList (Node* head) {if (!head){return head;for (Node* cur = head; cur != NULL ; cur = cur->next->next){new Node (cur->val, cur->next, NULL ); for (Node* cur = head; cur; cur = cur->next->next){if (cur->random){for (Node* cur = head; cur; cur = cur->next){NULL ;return newHead;
时间复杂度:O(n)
空间复杂度:O(1),不计入返回值。
归并排序(递归)
分割环节:找到链表中心链节点,从中心节点将链表断开,并递归进行分割。
归并环节:将递归后的链表进行两两归并,完成一遍后每个子链表长度加倍。重复进行归并操作,直到得到完整的链表。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 class Solution {public :ListNode* sortList (ListNode* head) {return mergeSort (head);ListNode* mergeSort (ListNode* head) {if (!head || !head->next){return head;while (fast->next && fast->next->next){nullptr ;return merge (mergeSort (left), mergeSort (right));ListNode* merge (ListNode* left, ListNode* right) {new ListNode ();while (left && right){if (left->val < right->val){else {return dummy->next;
时间复杂度:O(nlogn)
空间复杂度:O(logn),递归需要 O(logn) 的栈开销。
归并排序(迭代) 具体算法:
遍历链表,获取链表长度 length。
初始化步长 step=1。
循环直到 step≥length。
每轮循环,从链表头节点开始。
分割出两段长为 step 的链表,合并,把合并后的链表插到新链表的末尾。重复该步骤,直到链表遍历完毕。
把 step 扩大一倍。回到第 4 步。
迭代的方法有些难理解,晚上有时间再看吧。
分治法 如果只剩一个链表,就结束递归。然后合并两个链表,按照归并排序的方式合并。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 class Solution {public :ListNode* mergeKLists (vector<ListNode*>& lists) {int k = lists.size ();if (k == 0 ){return nullptr ;return mergeSort (lists, 0 , k-1 );ListNode* mergeSort (vector<ListNode*>& lists, int left, int right) {if (left == right){return lists[left];int mid = (left + right) >> 1 ;return merge (mergeSort (lists, left, mid), mergeSort (lists, mid+1 , right));ListNode* merge (ListNode* leftList, ListNode* rightList) {new ListNode ();while (leftList && rightList){if (leftList->val < rightList->val){else {return dummy->next;
时间复杂度:O(nlogk),其中 k 为 lists 的长度,n 为所有链表的节点数之和。每个节点参与链表合并的次数为 O(logk) 次,一共有 n 个节点,所以总的时间复杂度为 O(nlogk)。
空间复杂度:O(logk),递归栈消耗的空间。
优先队列 维护当前每个链表没有被合并的元素的最前面一个,k 个链表就最多有 k 个满足这样条件的元素,每次在这些元素里面选取 val 属性最小的元素合并到答案中。在选取最小元素的时候,可以用优先队列来优化这个过程。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Solution {public :ListNode* mergeKLists (vector<ListNode*>& lists) {auto cmp = [&](const ListNode* a, ListNode* b){return a->val > b->val;decltype (cmp)> heap (cmp);for (auto head : lists){if (head) heap.push (head);new ListNode ();while (!heap.empty ()){top ();pop ();if (node->next){push (node->next);return dummy->next;
时间复杂度:O(nlogk),其中 k 为 lists 的长度,n 为所有链表的节点数之和。
空间复杂度:O(k),最小堆中最多包含k个元素。
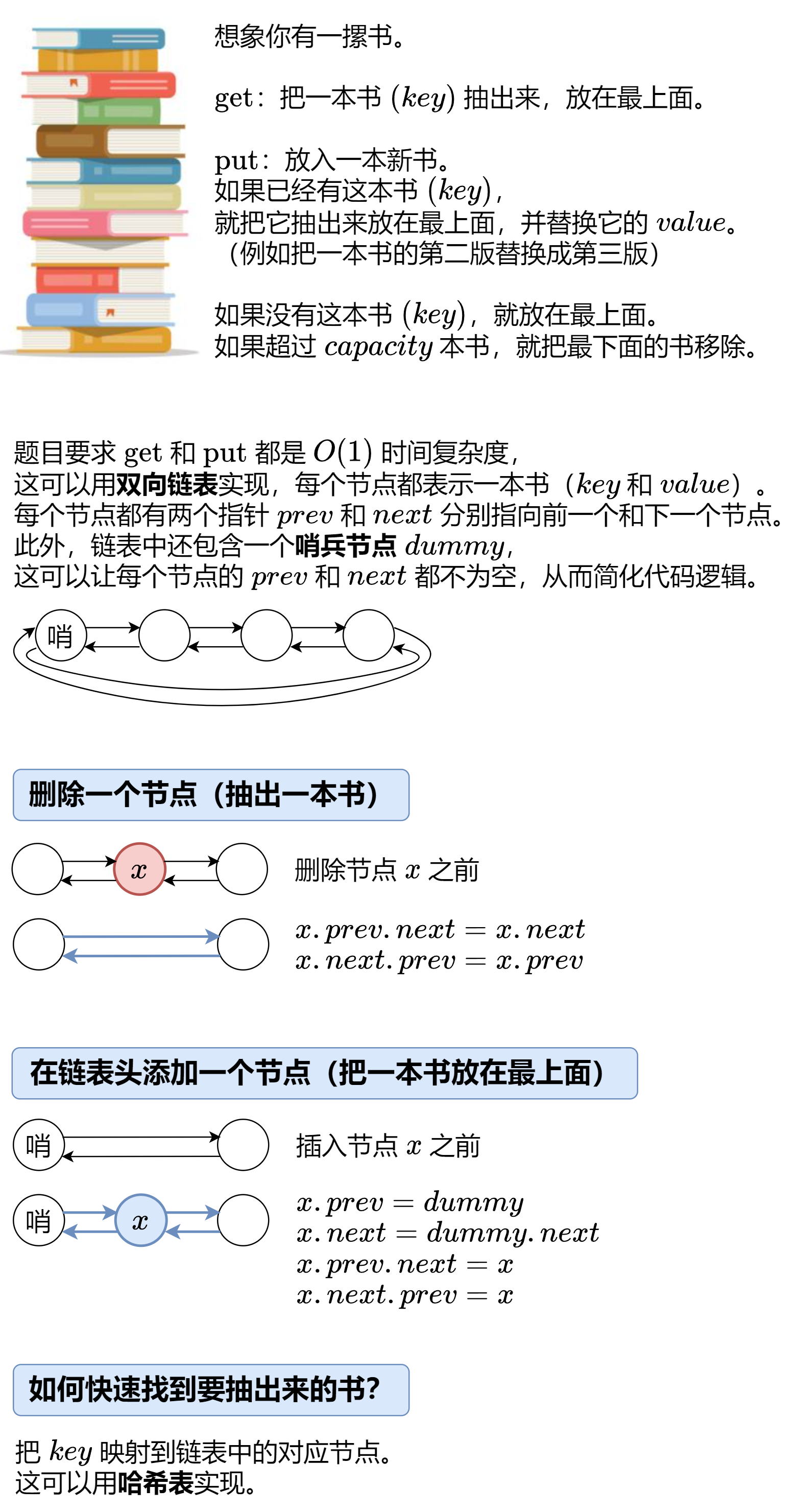
双向链表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 class Node {public :int key;int value;Node (int k = 0 , int v = 0 ) : key (k), value (v) {}class LRUCache {public :LRUCache (int capacity) : capacity (capacity) {new Node ();int get (int key) getNode (key);return node ? node->value : -1 ;void put (int key, int value) getNode (key);if (node){else {new Node (key, value);pushFront (hash[key]);if (hash.size () > capacity){erase (backNode->key);remove (backNode);delete backNode;private :int capacity;int , Node*> hash;void remove (Node* x) void pushFront (Node* x) Node* getNode (int key) {auto it = hash.find (key);if (it == hash.end ()){return NULL ;remove (node); pushFront (node); return node;
时间复杂度:所有操作均为 O(1)。
空间复杂度:O(min(p,capacity)),其中 p 为 put 的调用次数。
之后有时间可以练一下LFU缓存 。