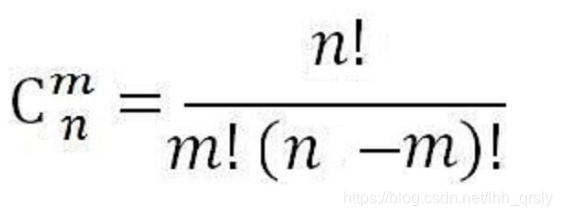07.04 第 088 ~ 100 题（第 13 ~ 16 天）

买股票的最佳时机

分析

初步考虑每次结算出在第i天买入在第j天售出所能获得的利润，且j> i，维护一个变量记录最大值。但是这样的时间复杂度是O(n)，无法通过所有的测试用例，因此进行优化。

假设股票在第i天售出，那么需要知道前i-1天中股票价格的最小值，用一个变量维护，因此只需一次遍历即可。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        int ans = 0;
        int minPrice = prices[0];

        for(int i = 1; i < n; i++){
            minPrice = min(minPrice, prices[i-1]);
            ans = max(ans, prices[i] - minPrice);
        }

        return ans;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

买股票的最佳时机II

分析

只要是上升趋势的都买，就能使利益最大化。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        int ans = 0;

        for(int i = 1; i < n; i++){
            if(prices[i] > prices[i-1]){
                ans += prices[i] - prices[i-1];
            }
        }

        return ans;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

最长递增子序列

动态规划

1. 划分阶段：按子序列结束的位置划分阶段。
2. 定义状态：dp[i]表示以nums[i]结尾的最大递增子序列长度。
3. 状态转移方程：枚举0 ~ i-1之间的数，如果nums[i] > nums[j]，则dp[i]才可能从dp[j]转移过来。即dp[i] = max(dp[i], dp[j] + 1)。
4. 初始条件：每个以nums[i]结尾的初始递增子序列长度为1，即它本身。
5. 返回结果：维护一个最大值变量。

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n, 1);

        int ans = 1;
        for(int i = 1; i < n; i++){
            for(int j = 0; j < i; j++){
                if(nums[i] > nums[j]){
                   dp[i] = max(dp[i], dp[j] + 1); 
                }
            }
            ans = max(ans, dp[i]);
        }

        return ans;
    }
};

• 时间复杂度：$O(n ^ 2)$
• 空间复杂度：O(n)

贪心+二分查找

• 维护一个数组 d[i] ，表示长度为 i 的最长上升子序列的末尾元素的最小值，用 len 记录目前最长上升子序列的长度，起始时 len 为 1，d[1]=nums[0]。
• 从前往后遍历数组 nums，在遍历到 nums[i] 时：
  • 如果 nums[i]>d[len] ，则直接加入到 d 数组末尾，并更新 len=len+1；
  • 否则，在 d 数组中二分查找，找到第一个比 nums[i] 小的数 d[k] ，并更新 d[k+1]=nums[i]。如果找不到说明所有的数都比 nums[i] 大，此时要更新 d[1].

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        int len = 1;

        // 定义d数组并初始化
        vector<int> d(n + 1, 0);
        d[len] = nums[0];

        // 遍历数字
        for(int i = 1; i < n; i++){
            if(nums[i] > d[len]){
                d[++len] = nums[i];
            }else{
                // 二分查找到第一个比nums[i]小的
                int left = 1, right = len, pos = 0;
                while(left <= right){
                    int mid = (left + right) >> 1;
                    if(d[mid] < nums[i]){
                        pos = mid;
                        left = mid + 1;
                    }else{
                        right = mid - 1;
                    }
                }
                d[pos + 1] = nums[i];
            }
        }
        return len;
    }
};

• 时间复杂度：O(nlogn)
• 空间复杂度：O(n)

也可以进行空间优化，在原地将找到的第一个比x小的数修改为x。在当前序列中找到一个位置，能够用 x 来代替（如果 x 比当前的位置的元素小）。这种做法是为了保持序列的最小性，有助于后续找到更长的递增子序列。

最长公共子序列

分析

1. 划分阶段：按照两个字符串的结尾位置进行阶段划分。
2. 定义状态：dp[i][j]等于以text1前i个字符和text2以前j个字符的子序列长度。
3. 状态转移方程：
   • 如果text1[i-1] == text2[j-1]，则dp[i][j] = dp[i-1][j-1] + 1；
   • 否则dp[i][j] = max(dp[i-1][j], dp[i][j-1])。
4. 初始条件：
   • dp[i][0] = dp[0][j] = 0；
5. 返回结果：dp[size1][size2]。

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int size1 = text1.size();
        int size2 = text2.size();
        vector<vector<int>> dp(size1 + 1, vector<int>(size2 + 1));

        for(int i = 1; i <= size1; i++){
            for(int j = 1; j <= size2; j++){
                if(text1[i-1] == text2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else{
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }

        return dp[size1][size2];
    }
};

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(n^2)$

最小路径和

分析

1. 划分阶段：按位置划分阶段。
2. 定义状态：dp[i][j]表示从(0,0)走到(i,j)的最小路径和。
3. 状态转移方程：dp[i][j] = min(dp[i-1][j], dp[i][j-1] + grid[i][j])。
4. 初始条件：dp[0][0] = grid[0][0]。
5. 返回结果：dp[m-1][n-1]。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n));
        dp[0][0] = grid[0][0];

        // 初始化
        for(int i = 1; i < m; i++){
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        for(int j = 1; j < n; j++){
            dp[0][j] = dp[0][j-1] + grid[0][j];
        }

        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
            }
        }

        return dp[m-1][n-1];
    }
};

• 时间复杂度：$O(m \times n)$
• 空间复杂度：$O(m \times n)$

编辑距离

分析

1. 划分阶段：按照两个字符串的结尾位置进行阶段划分。
2. 定义状态：dp[i][j]word1的前i个字符和word2的前j个字符表示最小操作数。
3. 状态转移方程：
   • 如果word1[i-1] == word2[j-1]，无需操作，dp[i][j] = dp[i-1][j-1]。
   • 否则，要么插入，要么删除，要么替换，即dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1。
4. 初始条件：dp[i][0] = i，dp[0][j] = j。
5. 返回结果：dp[size1][size2]。

class Solution {
public:
    int minDistance(string word1, string word2) {
        int size1 = word1.size();
        int size2 = word2.size();
        vector<vector<int>> dp(size1 + 1, vector<int>(size2 + 1));

        // 初始化
        for(int i = 0; i <= size1; i++){
            dp[i][0] = i;
        }
        for(int j = 0; j <= size2; j++){
            dp[0][j] = j;
        }

        for(int i = 1; i <= size1; i++){
            for(int j = 1; j <= size2; j++){
                if(word1[i-1] == word2[j-1]){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1;
                }
            }
        }
        return dp[size1][size2];
    }
};

• 时间复杂度：$O(m \times n)$
• 空间复杂度：$O(m \times n)$

不同路径

动态规划

1. 划分阶段：按位置划分阶段。
2. 定义状态：dp[i][j]表示机器人走到位置(i,j)总共有多少条不同的路径。
3. 状态转移方程：dp[i][j] = dp[i-1][j] + dp[i][j-1](i,j > 0)。
4. 初始条件：dp[0][0] = 1.
5. 返回结果：dp[m-1][n-1]。

class Solution {
public:
    int uniquePaths(int m, int n) {
        // 定义状态
        vector<vector<int>> dp(m, vector<int>(n));
        dp[0][0] = 1;
        // 循环遍历
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(i > 0){
                    dp[i][j] += dp[i-1][j];
                }
                if(j > 0){
                    dp[i][j] += dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

f(i,j) 仅与第 i 行和第 i−1 行的状态有关，因此我们可以使用滚动数组代替代码中的二维数组，使空间复杂度降低为 O(n)。

class Solution {
public:
    int uniquePaths(int m, int n) {
        // 定义状态
        vector<int> dp(n, 1);
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[j] += dp[j-1];
            }
        }
        return dp[n-1];
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(n)

组合数学

$C_{m+n-2}^{m-1} = \frac{(m+n-2)!}{(m-1)! (n-1)!} = \frac{(m+n-2)(m+n-3 … n)}{(m-1)!}$

class Solution {
public:
    int uniquePaths(int m, int n) {
        long long ans = 1;
        for(int x = n, y = 1; y < m; x++, y++){
            ans = ans * x / y;
        }
        return ans;
    }
};

• 时间复杂度：O(m)
• 空间复杂度：O(1)

乘积最大子数组

动态规划

这里的定义并不满足「最优子结构」,当前位置的最优解未必是由前一个位置的最优解转移得到的。根据正负性进行分类讨论：

• 当前位置如果是一个负数，那么就希望以它前一个位置结尾的某个段的积也是个负数，这样就可以负负得正，并且希望这个积尽可能「负得更多」，即尽可能小。可以再维护一个 $f_{min}(i)$，它表示以第 i 个元素结尾的乘积最小子数组的乘积。fmin[i] = min(nums[i], fmin[i-1]* nums[i], fmax[i-1]* nums[i])。
• fmax[i] = max(nums[i], fmax[i-1]* nums[i], fmin[i-1]* nums[i])。

可以进行空间优化，即用两个变量来维护fmin[i-1]和fmax[i-1]。

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int n = nums.size();
        // 定义状态
        int fmin = nums[0], fmax = nums[0], ans = nums[0];

        for (int i = 1; i < n; i++) {
            int tmax = fmax, tmin = fmin;
            fmax = max({tmax * nums[i], tmin * nums[i], nums[i]});
            fmin = min({tmin * nums[i], tmax * nums[i], nums[i]});
            ans = max(ans, fmax);
        }
        return ans;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

打家劫舍

动态规划

1. 定义状态：dp[i]表示当前能偷取的最大数值。
2. 状态转移方程：要么偷，即dp[i] = dp[i-2] + nums[i]，因为不能偷相邻的，要么不偷，即dp[i] = dp[i-1]。两者取较大。
3. 初始条件：dp[0] = nums[0]，如果n > 1则dp[1] = nums[1]。
4. 返回结果：max(dp[n-1], dp[n-2])。

空间优化：只用两个变量保存dp[i-1]和dp[i-2]。

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if(n == 1){
            return nums[0];
        }
        // 定义状态
        int prepre = nums[0], pre = max(prepre, nums[1]);
        for(int i = 2; i < n; i++){
            int tpre = pre;
            pre = max(prepre + nums[i], tpre);
            prepre = tpre;
        }

        return max(prepre, pre);
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

随机链表的复制

回溯 + 哈希表

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/

class Solution {
public:
    unordered_map<Node*, Node*> cachedNode;

    Node* copyRandomList(Node* head) {
        if(head == NULL){
            return NULL;
        }
        // 如果还没有为当前结点创建过副本
        if(!cachedNode.count(head)){
            Node* newHead = new Node(head->val);
            cachedNode[head] = newHead;
            newHead->next = copyRandomList(head->next);
            newHead->random = copyRandomList(head->random);
        }

        return cachedNode[head];
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

迭代 + 节点拆分

1. 首先将该链表中每一个节点拆分为两个相连的节点，例如对于链表 A→B→C，我们可以将其拆分为 A→A′→B→B ′→C→C ′。对于任意一个原节点 S，其拷贝节点 S ′即为其后继节点。
2. 这样，我们可以直接找到每一个拷贝节点S′的随机指针应当指向的节点，即为其原节点 S 的随机指针指向的节点 T 的后继节点T′。需要注意原节点的随机指针可能为空，我们需要特别判断这种情况。
3. 当我们完成了拷贝节点的随机指针的赋值，我们只需要将这个链表按照原节点与拷贝节点的种类进行拆分即可，只需要遍历一次。同样需要注意最后一个拷贝节点的后继节点为空，我们需要特别判断这种情况。

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/

class Solution {
public:
    Node* copyRandomList(Node* head) {
        // 边界处理
        if(head == NULL){
            return NULL;
        }
        // 复制每个节点
        for(Node* node = head; node != NULL; node = node->next->next){
            Node* newNode = new Node(node->val);
            newNode->next = node->next;
            node->next = newNode;
        }
        // 随机指针
        for(Node* node = head; node != NULL; node = node->next->next){
            Node* newNode = node->next;
            newNode->random = (node->random != NULL) ? node->random->next : NULL;
        }
        // 复原链表，拆分
        Node* newHead = head->next;
        for(Node* node = head; node != NULL; node = node->next){
            Node* newNode = node->next;
            node->next = node->next->next;
            newNode->next = (newNode->next != NULL) ? newNode->next->next : NULL;
        }
        return newHead;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

二叉树的序列化与反序列化

广度优先搜索

之前在刷剑指offer的时候用先序遍历做过，这里用层次遍历做。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:
    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        if (!root) return "#";

        string ans = "";
        queue<TreeNode*> que;
        que.push(root);

        while (!que.empty()) {
            TreeNode* node = que.front();
            que.pop();

            if (node) {
                ans += to_string(node->val) + ",";
                que.push(node->left);
                que.push(node->right);
            } else {
                ans += "#,";
            }
        }

        return ans;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        if (data == "#") return NULL;

        stringstream s(data);
        string strNode;
        getline(s, strNode, ',');

        TreeNode* root = new TreeNode(stoi(strNode));
        queue<TreeNode*> que;
        que.push(root);

        while (!que.empty()) {
            TreeNode* node = que.front();
            que.pop();

            if (getline(s, strNode, ',')) {
                if (strNode != "#") {
                    node->left = new TreeNode(stoi(strNode));
                    que.push(node->left);
                }
            }

            if (getline(s, strNode, ',')) {
                if (strNode != "#") {
                    node->right = new TreeNode(stoi(strNode));
                    que.push(node->right);
                }
            }
        }

        return root;
    }
};

// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

• 时间复杂度：O(n)
• 空间复杂度：O(n)

长度最小的子数组

滑动窗口

定义两个指针，右指针不断向右滑动，直至窗口内的和大于等于目标，则尝试收缩窗口，直到 sum < target，并更新最小长度，移动左指针。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int n = nums.size();
        int left = 0;
        int ans = INT_MAX;
        int sum = 0;

        for (int right = 0; right < n; ++right) {
            sum += nums[right];  // 增加右边界的值

            // 尝试收缩窗口，直到 sum < target
            while (sum >= target) {
                ans = min(ans, right - left + 1);
                sum -= nums[left++];
            }
        }

        // 如果没有找到满足条件的子数组，返回 0
        return ans == INT_MAX ? 0 : ans;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

前缀和+二分查找

这道题保证了数组中每个元素都为正，所以前缀和一定是递增的，得到前缀和之后，对于每个开始下标 i，可通过二分查找得到大于或等于 i 的最小下标 bound，使得 sums[bound]−sums[i−1]≥s，并更新子数组的最小长度（此时子数组的长度是 bound−(i−1)）。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int n = nums.size();
        int ans = INT_MAX;

        // 求前缀和
        vector<int> sums(n+1, 0);
        for(int i = 1; i <= n; i++){
            sums[i] = sums[i-1] + nums[i-1];
        }

        // 以每一个i-1为起点
        for(int i = 1; i <=n; i++){
            int tmp = target + sums[i-1];
            auto bound = lower_bound(sums.begin(), sums.end(), tmp);
            if(bound != sums.end()){
                ans = min(ans, static_cast<int>(bound - sums.begin()) - (i-1));
            }
            
        }
        return ans == INT_MAX ? 0 : ans;
    }
};

• 时间复杂度：O(nlogn)
• 空间复杂度：O(n)

单词拆分

动态规划

1. 划分阶段：按照单词结尾位置进行阶段划分。
2. 定义状态： 能否拆分为单词表的单词，可以分解为：前i个字符构成的字符串，能否分解为单词；剩余字符串，能否分解为单词。dp[i]表示前i个字符组成的字符串是否可以拆分成单词表的单词。
3. 状态转移数组：如果s[0:j]可以拆分，即dp[j]=true，并且s[j:i]出现在字典中，则dp[i] = true。如果s[0:j]不可以拆分，或者s[j:i]没有出现在字典中，则dp[i] = false。
4. 初始条件：长度为0的字符串可以拆分为单词，dp[0] = true。
5. 返回结果：dp[n]

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        int n = s.length();
        // 定义状态
        vector<bool> dp(n + 1, false);
        dp[0] = true;

        // 存入哈希表便于查找
        unordered_set<string> words;
        for(string& str : wordDict){
            words.insert(str);
        }

        // 填表
        for(int i = 1; i <= n; i++){
            // 枚举j
            for(int j = 0; j < i; j++){
                string sub = s.substr(j, i - j);
                if(dp[j] && words.count(sub) != 0){
                    dp[i] = true;
                }
            }
        }
        return dp[n];
    }
};

• 时间复杂度：$O(n^2)$
• 空间复杂度：O(n)

总结

至此，leetcode算法笔记从基础算法篇到面试篇下的内容都刷完了，题目较多地涉及到递归、二叉树、滑动窗口、动态规划等内容，虽然有很多题在剑指offer里都做过，但再次遇到时还是会思路不清晰。之后计划跟着灵神的题单继续刷，记得每周日把这一周刷得题目再复习一遍，然后可以参加一些周赛或者双周赛。白日梦想家停止幻想的关键就在于行动，加油！