07.01 第 051 ~ 072 题（第 01 ~ 04 天）

07.01 第 051 ~ 072 题（第 01 ~ 04 天）

无重复字符的最长子串

分析

使用哈希表+滑动窗口。如果当前字符没有在哈希表中出现过，就将其加入哈希表，右指针继续向右，right-left+1是当前长度，不断更新最大长度；否则不断向右滑动左窗口，直至遇到哈希表内没有当前元素，再把当前元素加入哈希表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int n = s.length();
        // 处理边界
        if(n == 0 || n == 1){
            return n;
        }
        // 定义哈希表，左右指针
        unordered_map<char, int> hash;
        int left = 0, right = 0;
        int ans = 0;
        // 遍历字符串
        while(right < n){
            if(hash.find(s[right]) == hash.end()){
                hash[s[right]] = 1;
            }else{
                hash[s[right]]++;
            }
            // 左指针滑动至没有重复字符
            while(hash[s[right]] > 1){
                hash[s[left]]--;
                left++;
            }
            ans = max(ans, right - left + 1);
            right++;
        }
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

最长回文子串

中心扩散

可以用从中心向两边扩展的方法，对每一个位置都进行这样的操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.length();
        // 维护当前长度和最大长度
        int len = 1, maxLen = 1;
        // 维护最长子串的起始指针
        int maxStart = 0;
        // 遍历字符串：
        for(int i = 0; i < n; i++){
            // 定义左右指针
            int left = i - 1, right = i + 1;
            // 偶数个，向左扩展
            while(left >= 0 && s[left] == s[i]){
                len++;
                left--;
            }
            // 向右扩展
            while(right < n && s[right] == s[i]){
                len++;
                right++;
            }
            // 奇数个，向两边扩展
            while(left >= 0 &&right < n && s[left] == s[right]){
                len += 2;
                left--;
                right++;
            }
            // 更新最大长度
            if(len > maxLen){
                maxLen = len;
                maxStart = left + 1;
            }
            len = 1;
        }
        return s.substr(maxStart, maxLen);
    }
};
  • 时间复杂度：$O(n^2)$
  • 空间复杂度：O(1)

动态规划

  1. 划分阶段：按照区间长度进行阶段划分。

  2. 定义状态：dp[i][j]表示s[i:j]是否是回文的。

  3. 状态转移方程：

    $s[i] = s[j], dp[i][j] = \begin{cases} true & j-i \leq 2 \cr dp[i+1][j - 1] & else \end{cases}$

  4. 初始条件：dp[i][j]=false.

  5. 返回结果：s[maxStart:maxStart+maxLen]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.length();
        int maxLen = 1;
        int maxStart = 0;
        // 定义状态数组
        vector<vector<bool>> dp(n, vector<bool>(n));
        // 枚举结束位置
        for(int j = 1; j < n; j++){
            // 枚举起始位置
            for(int i = 0; i < j; i++){
                if(s[i] == s[j]){
                    if(j - i <= 2){
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i+1][j-1];
                    }                    
                }
                // 更新最大长度
                if(dp[i][j] && j - i + 1 > maxLen){
                    maxLen = j - i + 1;
                    maxStart = i;
                }
            }
        }
        // 返回结果
        return s.substr(maxStart, maxLen);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

Manacher 算法

字符串转换整数

分析

  1. 空格：读入字符串并丢弃无用的前导空格（” “）
  2. 符号：检查下一个字符（假设还未到字符末尾）为 ‘-‘ 还是 ‘+’。如果两者都不存在，则假定结果为正。
  3. 转换：通过跳过前置零来读取该整数，直到遇到非数字字符或到达字符串的结尾。如果没有读取数字，则结果为0。
  4. 舍入：如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 −231 的整数应该被舍入为 −231 ，大于 231 − 1 的整数应该被舍入为 231 − 1 。
  5. 读取在第一个非数字字符处停止。

自己写的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int myAtoi(string s) {
        int n = s.length();
        int flag = 1;
        // 跳过空格
        int i = 0;
        while(i < n && s[i] == ' ') i++;
        // 获取符号
        if(s[i] == '-' || s[i] == '+'){
            flag = s[i] == '-' ? -1 : 1;
            i++;
        }
        // 跳过前导0
        long long num = 0;
        while(i < n && isdigit(s[i])){
            num = num * 10 + (long long)(s[i] - '0');
            i++;
            // 舍入
            if(flag * num > INT_MAX) return INT_MAX;
            if(flag * num < INT_MIN) return INT_MIN;
        }
        num *= flag;
        return num;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

自动机

反转字符串中的单词

分析

用一个额外的字符串处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    string reverseWords(string s) {
        int n = s.length();
        string ans = "";
        reverse(s.begin(), s.end());
        // 遍历
        int i = 0;
        while(1){
            if(i == n){
                break;
            }
            // 寻找第一个不是空格的
            while(i < n && s[i] == ' ') i++;
            // 截断单词
            string tmp;
            while(i < n && s[i] != ' '){
                tmp += s[i];
                i++;
            }
            reverse(tmp.begin(), tmp.end());
            if(tmp != ""){
                ans += tmp + " ";
            }
        }
        // 返回结果
        ans = ans.substr(0, ans.size()-1);
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

字符串相乘

分析

模拟。可以先将字符串反转，从前向后就是从低位到高位的运算。可以在高位的计算结果后补零，这样方便结果相加。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    string multiply(string num1, string num2) {
        if (num1 == "0" || num2 == "0") return "0";  // 处理边界情况

        int n1 = num1.length();
        int n2 = num2.length();
        vector<int> result(n1 + n2, 0);  // 初始化结果数组

        // 反向遍历字符串进行乘法
        for (int i = n1 - 1; i >= 0; --i) {
            for (int j = n2 - 1; j >= 0; --j) {
                int mul = (num1[i] - '0') * (num2[j] - '0');
                int sum = mul + result[i + j + 1];  // 当前位的乘法结果加上之前的值
                result[i + j + 1] = sum % 10;  // 存储当前位
                result[i + j] += sum / 10;  // 处理进位
            }
        }

        // 构建结果字符串
        string res = "";
        for (int num : result) {
            if (!(res.empty() && num == 0)) {  // 跳过前导零
                res += to_string(num);
            }
        }

        return res.empty() ? "0" : res;  // 如果结果为空则返回"0"
    }
};
  • 时间复杂度：O(mn)
  • 空间复杂度：O(m+n)

最长公共前缀

分析

纵向遍历，从第一个字符开始，比较每一个字符串的第一个字符是否相等。若相等，则比较第二个字符，若不相等，则结束循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        string s0 = strs[0];
        for(int j = 0; j < s0.size(); j++){
            for(string& s : strs){
                if(j == s.size() || s[j] != s0[j]){
                    return s0.substr(0, j);
                }
            }
        }
        return s0;
    }
};
  • 时间复杂度：O(mn)
  • 空间复杂度：O(1)

二叉树的前序遍历

迭代

  1. 判断二叉树是否为空，为空则直接返回。
  2. 初始化维护一个栈，将根节点入栈。
  3. 当栈不为空时：
    • 弹出栈顶元素 node，并访问该元素。
    • 如果 node 的右子树不为空，则将 node 的右子树入栈。
    • 如果 node 的左子树不为空，则将 node 的左子树入栈。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;
        // 处理边界
        if(!root){
            return ans;
        }
        stack<TreeNode*> stk;
        stk.push(root);
        while(!stk.empty()){
            TreeNode* node = stk.top(); // 弹出栈顶
            stk.pop();
            ans.push_back(node->val);   // 访问栈顶
            if(node->right){
                stk.push(node->right);
            }
            if(node->left){
                stk.push(node->left);
            }
        }
        return ans;
    }
};

Morris遍历

在二叉树遍历的深度优先遍历中，分析了如何用递归和非递归方式实现遍历二叉树，但是那些方法都无法做到空间复杂度为 O(1)，对于递归方法，遍历时用到了函数栈，而对于非递归方法，则是直接申请了栈，这两种方法的空间复杂度均与树的高度相关，设树的高度为 h，则空间复杂度为 O(h)。

二叉树上的很多节点都有大量的空闲指针（如叶节点就有两个空闲指针），比如某些节点没有右孩子节点，那么这个节点的 right 指针就指向 null，我们将之称为空闲状态，而Morris遍历就是使用了这些空闲指针。

  1. 若 cur == null，则过程停止，否则继续下面的过程；
  2. 若 cur 无左子树，则令 cur = cur.right；
  3. 若 cur 有左子树，则找到 cur 左子树上最右的节点，记作 mostRight：
    • 若 mostRight.right == null，则令 mostRight.right = cur，即让 mostRight 的 right 指针指向当前节点 cur，然后令 cur = cur.left；
    • 若 mostRight.right == cur， 则令 mostRight.right = null，即让 mostRight 的 right 指针指向空，然后令 cur = cur.right。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;
        TreeNode* cur = root;
        while(cur){
            // 无左子树，则指向右子树
            if(!cur->left){
                ans.push_back(cur->val);
                cur = cur->right;
            }else{
                // 有左子树，找到左子树最右边的节点
                TreeNode* leftNode = cur->left;
                while(leftNode->right && leftNode->right != cur){
                    leftNode = leftNode->right;
                }
                // 如果指向空
                if(leftNode->right == NULL){
                    ans.push_back(cur->val);
                    leftNode->right = cur;
                    cur = cur->left;
                }else if(leftNode->right == cur){
                    leftNode->right = NULL;
                    cur = cur->right;
                }
            }
        }
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

二叉树的中序遍历

迭代

  1. 判断二叉树是否为空，为空则直接返回。
  2. 初始化维护一个栈.
  3. 当栈不为空或当前结点不为空：
    • 当当前节点不为空，将当前节点指向它的左子树，并入栈。
    • 弹出栈顶元素 node，并访问该元素。
    • 尝试访问右子树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        // 处理边界
        if(!root){
            return ans;
        }
        // 维护栈
        stack<TreeNode*> stk;
        while(root || !stk.empty()){
            while(root){
                stk.push(root);
                root = root->left;
            }
            // 当栈不为空
            root = stk.top();
            stk.pop();    
            ans.push_back(root->val);   // 访问当前元素            
            // 尝试访问右子树
            root = root->right;
        }
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

Morris遍历

  1. 若 cur == null，则过程停止，否则继续下面的过程；
  2. 若 cur 无左子树，则访问当前元素，并令 cur = cur.right；
  3. 若 cur 有左子树，则找到 cur 左子树上最右的节点，记作 mostRight：
    • 若 mostRight.right == null，则令 mostRight.right = cur，即让 mostRight 的 right 指针指向当前节点 cur，然后令 cur = cur.left；
    • 若 mostRight.right == cur， 说明我们已经遍历完的左子树，则访问当前元素，并令 mostRight.right = null，即让 mostRight 的 right 指针指向空，然后令 cur = cur.right。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        while(root){
            // 如果左子树为空
            if(root->left == NULL){
                ans.push_back(root->val);
                root = root->right;
            }else{
                // 找到 cur 左子树上最右的节点
                TreeNode* leftNode = root->left;
                while(leftNode->right && leftNode->right != root){
                    leftNode = leftNode->right;
                }
                // 指向空，遍历左子树
                if(leftNode->right == NULL){
                    leftNode->right = root;
                    root = root->left;
                }else{
                    // 左子树已经遍历完
                    ans.push_back(root->val);
                    leftNode->right = NULL;
                    root = root->right;
                }
            }
        }
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

二叉树的层序遍历

分析

使用一个队列辅助。当队列不为空，弹出节点，将其左右子树加入队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        vector<vector<int>> ans;
        if(root == nullptr){
            return ans;
        }
        
        que.push(root);
        while(!que.empty()){
            int curSize = que.size();
            vector<int> cur;
            for(int i = 0; i < curSize; i++){
                TreeNode* node = que.front();
                cur.push_back(node->val);
                que.pop();

                if(node->left){
                    que.push(node->left);
                }
                if(node->right){
                    que.push(node->right);
                }                
            }
            ans.push_back(cur);
        }
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

二叉树的锯齿形层序遍历

分析

反转偶数层的数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        if(root == nullptr){
            return ans;
        }
        queue<TreeNode*> que;
        que.push(root);   
        
        while(!que.empty()){
            int n = que.size();
            vector<int> cur;
            for(int i = 0; i < n; i++){
                TreeNode* node = que.front();
                que.pop();
                cur.push_back(node->val);   // 访问当前元素
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            // 反转偶数层的
            if(ans.size() % 2 == 1){
                reverse(cur.begin(), cur.end());
            }
            ans.push_back(cur);
        }
        return ans;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

二叉树的最近公共祖先

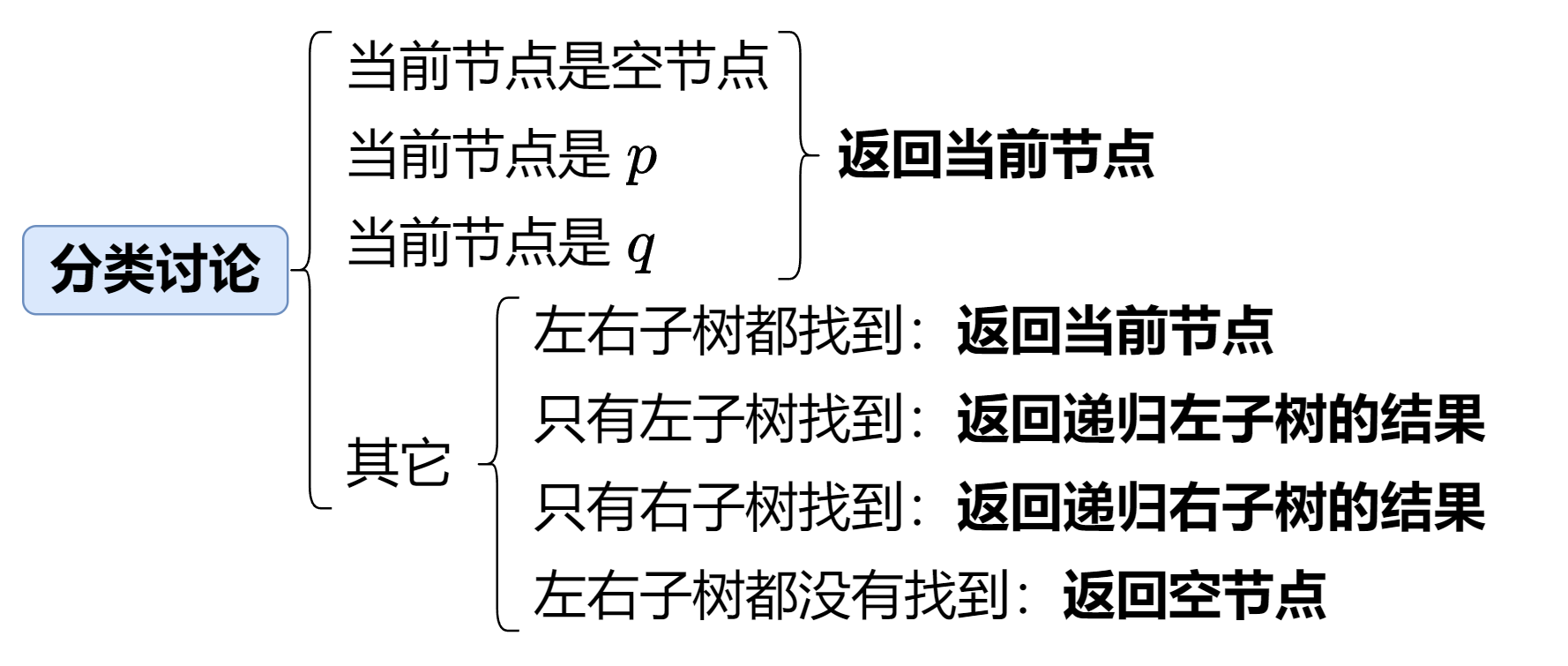
分析

Alt text

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 返回当前节点
        if(root == NULL || root == p || root == q){
            return root;
        }
        // 递归
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        // 如果两边都能找到，公共最先就是当前节点
        if(left && right){
            return root;
        } 
        // 如果左边能找到
        if(left){
            return left;
        }else{
            return right;
        }
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)，最坏情况下，二叉树是一条链，因此递归需要 O(n) 的栈空间。

二叉搜索树的最近公共祖先

分析

  • 如果p和q都小于当前节点值，则递归左子树。
  • 如果p和q都大于当前节点值，则递归右子树。
  • 如果分别位于不同子树上，则返回当前节点值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(p->val < root->val && q->val < root->val){
            return lowestCommonAncestor(root->left, p, q);
        }
        if(p->val > root->val && q->val >root->val){
            return lowestCommonAncestor(root->right, p, q);
        }
        return root;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)，最坏情况下，二叉搜索树退化成一条链（注意题目没有保证它是平衡树），因此递归需要 O(n) 的栈空间。

二叉树的最大深度

分析

如果当前节点为空，返回0.否则递归左右子树，取较大值，再+1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr){
            return 0;
        }
        int left = maxDepth(root->left);
        int right = maxDepth(root->right);
        return max(left, right) + 1;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)，最差情况下二叉树的高度为n，递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。

这道题也可以用层序遍历的思路去做，在每遍历完一层的时候，ans+1.

把上面的动态规划、马拉车、自动机方法学习一下。

算法笔记 > 面试篇
#leetcode-notes
07.01 第 051 ~ 072 题（第 01 ~ 04 天）
http://example.com/2024/11/01/posts/0701/
作者
Xuan Yang
发布于
2024年11月1日
许可协议