0601练习题目

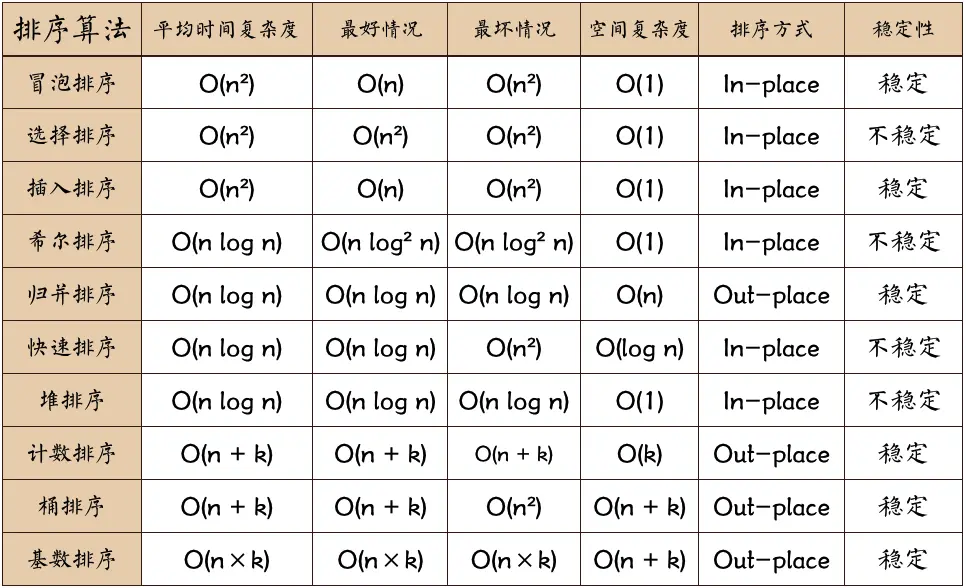
06.01第 001 ~ 012 题（第 01 ~ 04 天）

螺旋矩阵

分析

对矩阵进行模拟，每次更新边界位置，初始时向右走，当i == right，开始调整方向向下走，此时对i进行枚举，当i == down，调整方向向左走，枚举j，当i == left，调整方向向上走，对i进行枚举，当i == up，再次向右走。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        vector<int> res;
        // 定义边界
        int up = 0, down = m-1, left = 0, right = n-1;
        // 循环遍历
        while(true){
            // 向右走
            for(int i = left; i <= right; i++){
                res.push_back(matrix[up][i]);
            }
            // 向下走
            up += 1;
            if(up > down){
                break;
            }
            for(int i = up; i <= down; i++){
                res.push_back(matrix[i][right]);
            }
            // 向左走
            right -= 1;
            if(left > right){
                break;
            }
            for(int i = right; i >= left; i--){
                res.push_back(matrix[down][i]);
            }
            // 向上走
            down -= 1;
            if(up > down){
                break;
            }
            for(int i = down; i >= up; i--){
                res.push_back(matrix[i][left]);
            }
            // 循环往复
            left += 1;
            if(left > right){
                break;
            }
        }
        return res;
    }
};
  • 时间复杂度：$O(m \times n)$
  • 空间复杂度：$O(m \times n)$，如果算上答案数组的空间占用。

旋转图像

分析

对于位置(i,j)上的元素，其旋转后会放置在(j,n-i-1)的位置上，而原本(j,n-i-1)的位置上，会旋转到(n-i-1,n-j-1)；(n-i-1,n-j-1)会旋转到(n-j-1, i)，(n-j-1, i)会旋转到(i, j)。因此只需要一个临时变量存储循环中的元素即可。总结为：

1
2
3
4
5
temp = matrix[i][j]
matrix[i][j] = matrix[n-j-1][i]
matrix[n-j-1][i] = matrix[n-i-1][n-j-1]
matrix[n-i-1][n-j-1] = matrix[j][n-i-1]
matrx[j][n-i-1] = temp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for(int i = 0; i < n / 2; i++){
            for(int j = 0; j < (n+1) / 2; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n-j-1][i];
                matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
                matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
                matrix[j][n-i-1] = temp;
            }
        }        
    }
};
  • 时间复杂度：$O(n^2)$
  • 空间复杂度：O(1)

还可以通过一次水平翻转swap(matrix[i][j], matrix[n-i-1][j]) + 一次主对角线翻转swap(matrix[i][j], matrix[j][i])得到，此处不再赘述。

数组中的第k个最大元素

这道题之前做过很多次，大体思路是对数组进行降序（升序）排序，返回第k-1（n-k）个元素，排序方法主要是快排和堆排。这次要把快排和堆排的代码记住。

快速排序

使用快速排序在每次调整时，都会确定一个元素的最终位置，且以该元素为界限，将数组分成了左右两个子数组，左子数组中的元素都比该元素小，右子树组中的元素都比该元素大。

这样，只要某次划分的元素恰好是第k个下标就找到了答案。并且我们只需关注第k个最大元素所在区间的排序情况，与第k个最大元素无关的区间排序都可以忽略。这样进一步减少了执行步骤。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        int index = quickSelect(nums, 0, nums.size()-1, k);
        return nums[index];
    }
    // 分区函数
    int partion(vector<int>& nums, int left, int right){
        // 选择左边界元素作为基准元素
        int pivot = nums[left];
        // 初始化左右指针
        int i = left;
        int j = right + 1;
        // 开始分区
        while(1){
            // 从左往右找到第一个大于等于基准元素的元素
            while(++i < right && nums[i] < pivot);
            // 从右往左找到第一个小于等于基准元素的元素
            while(--j > left && nums[j] > pivot);
            // 如果左右指针相遇，则分区完成
            if(i >= j){
                break;
            }
            // 交换不符合条件的元素
            swap(nums[i], nums[j]);
        }
        // 将基准元素放置在正确的位置上
        swap(nums[left], nums[j]);
        // 返回基准元素的位置
        return j;
    }
    // 快速选择
    int quickSelect(vector<int>& nums, int left, int right, int k){
        // 分区并获取基准元素的位置
        int pivot = partion(nums, left, right);
        // 将 k 转换为数组下标
        int target = nums.size() - k;
        // 如果基准元素的位置就是目标位置，则返回该元素
        if(pivot == target){
            return pivot;
        }
        // 如果基准元素的位置小于目标位置，则在右侧继续查找
        else if(pivot < target){
            return quickSelect(nums, pivot+1, right, k);
        }
        // 如果基准元素的位置大于目标位置，则在左侧继续查找
        else{
            return quickSelect(nums, left, pivot-1, k);
        }
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(logn)

堆排序

如果能够找出 k 个最大的数字，那么第 k 大的数字就是这 k 个最大数字中最小的一个。由于每次都需要找出 k 个数字中的最小值，因此可以把这 k 个数字保存到最小堆中。首先构建最小堆，将数组的前 k 个元素插入到最小堆中。最小堆是一个完全二叉树，树中每个节点的值都小于或等于其子节点的值。然后遍历数组中剩下的元素，如果当前元素大于堆顶元素（最小堆中的最小值），则将堆顶元素替换为当前元素，并进行堆调整（向下调整）以保持最小堆的性质。遍历完成后，最小堆中的堆顶元素就是数组中的第 K 大元素。

  • minHeapify函数：用于调整以节点 i 为根的子树，使其满足小根堆的性质。它首先获取节点 i的左右子节点索引，然后找出其中最小的节点索引，如果该最小节点索引不等于当前节点索引 i，则交换当前节点和最小节点的值，并继续递归调整以最小节点为根的子树。
  • buildMinHeap函数：用于建立小根堆。它从最后一个非叶子节点开始，依次向前调整节点，保证以每个节点为根的子树都是小根堆。
  • heapSelect函数：首先构建一个大小为 k 的最小堆（只包含前 k 个元素）。然后遍历数组的剩余部分（从第 k 个元素到最后一个元素），如果当前元素比堆顶元素大，则将其与堆顶元素交换，并调整堆。最后，堆顶元素即为第 k 大的元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        return heapSelect(nums, k);
    }
    // 小根堆操作：将以节点 i 为根的子树进行小根堆调整
    void minHeapify(vector<int>& nums, int i, int heapSize){
        // 获取左右子节点索引和当前节点索引
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int smallest = i;
        // 如果左子节点存在且小于当前节点，则更新最小节点索引
        if(left < heapSize && nums[left] < nums[smallest]){
            smallest = left;
        }
        // 如果右子节点存在且小于当前节点或左子节点，则更新最小节点索引
        if(right < heapSize && nums[right] < nums[smallest]){
            smallest = right;
        }
        // 如果最小节点索引不等于当前节点索引，则交换当前节点和最小节点，并继续调整最小堆
        if(smallest != i){
            swap(nums[smallest], nums[i]);
            minHeapify(nums, smallest, heapSize);
        }
    }
    // 小根堆操作：建立小根堆
    void buildMinHeap(vector<int>& nums, int heapSize){
        // 从最后一个非叶子节点开始，依次向前调整节点，保证以每个节点为根的子树都是小根堆
        for(int i = heapSize / 2; i >= 0; i--){
            minHeapify(nums, i, heapSize);
        }
    }
    // 基于堆排序的选择方法
    int heapSelect(vector<int>& nums, int k){
        int heapSize = nums.size();
        // 构建一个大小为K的最小堆
        buildMinHeap(nums, k);
        // 处理剩余元素
        for(int i = k; i < heapSize; i++){
            // 如果当前元素比堆顶元素大，则替换堆顶元素
            if(nums[i] > nums[0]){
                swap(nums[0], nums[i]);
                minHeapify(nums, 0, k);
            }
        }
        return nums[0];
    }
};
  • 时间复杂度：$O(n \times \log n)$
  • 空间复杂度：堆选择算法需要一个大小为 k 的额外数组来存储堆，因此其空间复杂度为 O(k)。

排序数组

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        quickSort(nums, 0, nums.size()-1);
        return nums;
    }
    // 分区函数
    int partion(vector<int>& nums, int left, int right){
        // 选择基准元素
        int pivot = nums[left];
        // 初始化左右指针
        int i = left, j = right + 1;
        // 开始分区
        while(1){
             // 从左往右找到第一个大于等于基准元素的元素
             while(++i < right && nums[i] < pivot);
              // 从右往左找到第一个小于等于基准元素的元素
              while(--j > left && nums[j] > pivot);
              // 如果左右指针相遇，则分区完成
              if(i >= j){
                break;
              }
              // 交换不在位置的元素
              swap(nums[i], nums[j]);
        }
        // 将pivot放到正确位置
        swap(nums[left], nums[j]);
        // 返回基准元素的位置
        return j;
    }
    // 快速排序
    void quickSort(vector<int>&nums, int left, int right){
        if(left < right){
            // 划分数组
            int pivot = partion(nums, left, right);
            // 对两边数组进行快排
            quickSort(nums, left, pivot-1);
            quickSort(nums, pivot+1, right);
        }
    }
};
  • 时间复杂度：$O(n \times \log n)$
  • 空间复杂度：O(logn)

堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        int heapSize = nums.size();
        // 建立大根堆
        buildHeap(nums, heapSize);
        for(int i = heapSize - 1; i >= 0; i--){
            // 每次将堆顶（最大值）与当前堆的最后一个元素交换
            swap(nums[0], nums[i]);
            // 重新调整堆，排除已排序的最后一个元素
            heapSize--;
            maxHeapify(nums, 0, heapSize);
        }
        return nums;
    }
    // 调整堆
    void maxHeapify(vector<int>& nums, int i, int heapSize){
        // 计算左右子节点
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;
        // 更新最大节点索引
        if(left < heapSize && nums[left] > nums[largest]){
            largest = left;
        }
        if(right < heapSize && nums[right] > nums[largest]){
            largest = right;
        }
        // 如果最大节点索引不等于当前节点索引，则交换当前节点和最大节点，并继续调整最大堆
        if(largest != i){
            swap(nums[largest], nums[i]);
            maxHeapify(nums, largest, heapSize);
        }
    }
    // 建立大根堆
    void buildHeap(vector<int>& nums, int heapSize){
        // 从最后一个非叶子节点开始，依次向前调整节点，保证以每个节点为根的子树都是大根堆
        for(int i = heapSize / 2; i >= 0; i--){
            maxHeapify(nums, i, heapSize);
        }
    }
};
  • 时间复杂度：O(nlogn)
  • 空间复杂度：O(1)（忽略递归栈的空间）或 O(log n)（如果考虑递归栈空间）

排序算法总结

合并两个有序数组

分析

从前向后遍历的话，nums1的值可能会被覆盖，所以考虑从后向前遍历，不断比较nums1和nums2的值并放入nums1的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int i = m-1, j = n-1, k = m+n-1;
        while(i >= 0 && j >= 0){
            if(nums1[i] < nums2[j]){
                nums1[k--] = nums2[j--];
            }
            else{
                nums1[k--] = nums1[i--];
            }
        }
        while(i >= 0){
            nums1[k--] = nums1[i--];
        }
        while(j >= 0){
            nums1[k--] = nums2[j--];
        }
    }
};
  • 时间复杂度：$O(m + n)$
  • 空间复杂度：O(1)

多数元素

分治法

最直观的解法是用哈希表，这里用分治法来解决，题解中还有一种投票算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        return getMod(nums, 0, nums.size()-1);
    }
    int getMod(vector<int>& nums, int left, int right){
        // 只有一个元素
        if(left == right){
            return nums[left];
        }
        // 获取左右两部分的多数元素
        int mid = left + (right - left) / 2;
        int leftMod = getMod(nums, left, mid);
        int rightMod = getMod(nums, mid + 1, right);
        // 相等直接返回
        if(leftMod == rightMod){
            return leftMod;
        }
        // 否则进行计数
        int leftModCnt = 0, rightModCnt = 0;
        for(int i = left; i <= right; i++){
            if(nums[i] == leftMod){
                leftModCnt++;
            }
            else if(nums[i] == rightMod){
                rightModCnt++;
            }
        }
        return leftModCnt > rightModCnt ? leftMod : rightMod;
    }
};
  • 时间复杂度：$O(n \times \log n)$
  • 空间复杂度：$O(\log n)$

投票算法

如果我们把众数记为 +1，把其他数记为 −1，将它们全部加起来，显然和大于 0，从结果本身我们可以看出众数比其他数多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int cadidate = -1;
        int count = 0;
        for(int num : nums){
            if(num == cadidate){
                count++;
            }
            else if(--count < 0){
                cadidate = num;
                count = 1;
            }
        }
        return cadidate;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

只出现一次的数字

分析

数字逐个异或得到的结果就是这个数字，因为俩俩异或的结果是0.

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int res = 0;
        for(int num : nums){
            res ^= num;
        }
        return res;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

合并区间

分析

先按开始时间进行排序，然后逐个比较，如果前一个区间的结束时间大于后一个区间的开始时间，则将两个区间合并。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        // 对所有区间按开始时间进行排序
        sort(intervals.begin(), intervals.end());
        vector<vector<int>> res = {intervals[0]};
        // 逐个遍历区间
        for(int i = 1; i < intervals.size(); i++){
            if(res.back()[1] >= intervals[i][0]){
                res.back()[1] = max(intervals[i][1], res.back()[1]);
            }
            else{
                res.push_back(intervals[i]);
            }
        }
        return res;
    }
};
  • 时间复杂度：O(nlogn)，排序消耗的时间。
  • 空间复杂度：O(n)，结果数组。

最大数

分析

将所有数字按照最高位-最低位的大小进行排序，排序后组成的字符串就是结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    static bool compare(const int &num1, const int &num2) {
        string str1 = to_string(num1) + to_string(num2);
        string str2 = to_string(num2) + to_string(num1);
        return str1 > str2;
    }

    string largestNumber(vector<int>& nums) {
        sort(nums.begin(), nums.end(), compare);
        // 如果最大值是 0，直接返回 "0"
        if (nums[0] == 0) return "0";
        
        string res = "";
        for(int num : nums){
            res += to_string(num);
        }
        return res;
    }
};
  • 时间复杂度：O(nlogn)
  • 空间复杂度：O(n)

二分查找

分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int low = 0;
        int high = nums.size() - 1;
        while(low <= high){
            int mid = (low + high) / 2;
            if(nums[mid] == target){
                return mid;
            }
            else if(nums[mid] > target){
                high = mid - 1;
            }
            else{
                low = mid + 1;
            }
        }
        return -1;
    }
};
  • 时间复杂度：O(logn)
  • 空间复杂度：O(1)

在排序数组中查找元素的第一个和最后一个位置

分析

题目要求时间复杂度为O(logn)，所以使用二分法。在找到目标，即nums[mid] == target后，再以mid为中心向两边查找起始位置和结束位置。但在找到目标元素后，通过 while 循环向两边扩展，这样的复杂度接近 O(n)。可以通过两次独立的二分查找分别找到目标值的左边界和右边界。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if (nums.empty()) {
            return {-1, -1};
        }
        
        int left = findLeftBoundary(nums, target);
        int right = findRightBoundary(nums, target);
        
        // 如果左边界大于右边界，说明没有找到目标值
        if (left > right) {
            return {-1, -1};
        }
        
        return {left, right};
    }

private:
    // 查找左边界
    int findLeftBoundary(const vector<int>& nums, int target) {
        int low = 0, high = nums.size() - 1;
        while (low <= high) {
            int mid = low + (high - low) / 2;
            if (nums[mid] >= target) {
                high = mid - 1;  // 向左收缩范围
            } else {
                low = mid + 1;
            }
        }
        // 返回左边界
        return (low < nums.size() && nums[low] == target) ? low : -1;
    }

    // 查找右边界
    int findRightBoundary(const vector<int>& nums, int target) {
        int low = 0, high = nums.size() - 1;
        while (low <= high) {
            int mid = low + (high - low) / 2;
            if (nums[mid] <= target) {
                low = mid + 1;  // 向右收缩范围
            } else {
                high = mid - 1;
            }
        }
        // 返回右边界
        return (high >= 0 && nums[high] == target) ? high : -1;
    }
};
  • 时间复杂度：O(logn)
  • 空间复杂度：O(1)

寻找旋转排序数组中的最小值

分析

数组经过「旋转」之后，会有两种情况，第一种就是原先的升序序列，另一种是两段升序的序列。第一种的最小值在最左边。第二种最小值在第二段升序序列的第一个元素。

二分法：left和right分别指向数组首尾。计算mid:

  • 如果nums[mid] > nums[right]，则最小值一定在mid右侧；
  • 否则一定在mid或者mid的左侧。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findMin(vector<int>& nums) {
        int left = 0, right = nums.size() - 1;
        while(left < right){
            int mid = (left + right) / 2;
            if(nums[mid] > nums[right]){
                left = mid + 1;
            }
            else{
                right = mid;
            }
        }
        return nums[left];
    }
};
  • 时间复杂度：O(logn)
  • 空间复杂度：O(1)

寻找旋转排序数组中的最小值II

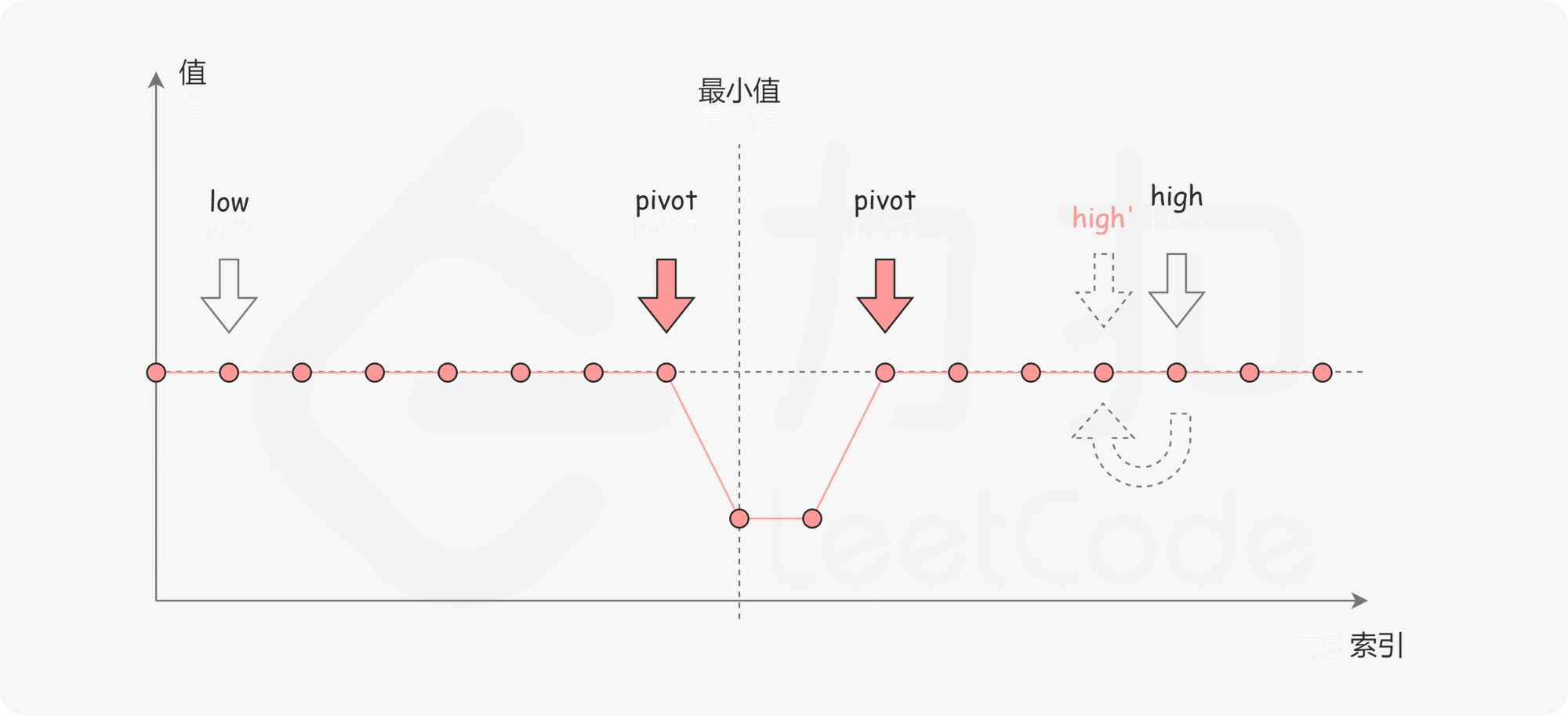
分析

与上一题类似，但 nums 可能包含重复元素。考虑数组中的最后一个元素 x：在最小值右侧的元素，它们的值一定都小于等于 x；而在最小值左侧的元素，它们的值一定都大于等于 x。

  • 如果nums[mid] < nums[right]，则mid是最小值或者在最小值右侧，因此可以忽略右边部分，更新right = mid。
  • 如果nums[mid] > nums[right]，则mid在最小值左侧，可以忽略左边部分，更新left = mid + 1。
  • 如果两者相等，则需要更新右端点值，如图所示：
    Alt text
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int findMin(vector<int>& nums) {
        int left = 0;
        int right = nums.size() - 1;
        while(left < right){
            int mid = (left + right) / 2;
            if(nums[mid] < nums[right]){
                right = mid;
            }
            else if(nums[mid] > nums[right]){
                left = mid + 1;
            }
            else{
                right--;
            }
        }
        return nums[left];
    }
};
  • 时间复杂度：平均时间复杂度为O(logn)，最坏情况下所有元素都相等，时间复杂度为O(n)。
  • 空间复杂度：O(1)

总结

第一部分的面试题比较简单，主要是模拟、排序、二分查找的题目，对于排序的题目，最好的方法是快排和堆排，其他的排序方法之后也要再敲一遍。二分查找要注意分析每次更新左右端点的方式，注意临界点。

算法笔记 > 面试篇
#leetcode-notes
0601练习题目
http://example.com/2024/10/14/posts/0601/
作者
Xuan Yang
发布于
2024年10月14日
许可协议