05.04 区间DP和树形DP
区间动态规划:线性 DP 的一种,简称为「区间 DP」。以「区间长度」划分阶段,以两个坐标(区间的左、右端点)作为状态的维度。一个状态通常由被它包含且比它更小的区间状态转移而来。
区间 DP 的主要思想就是:先在小区间内得到最优解,再利用小区间的最优解合并,从而得到大区间的最优解,最终得到整个区间的最优解。
根据小区间向大区间转移情况的不同,常见的区间 DP 问题可以分为两种:
- 单个区间从中间向两侧更大区间转移的区间 DP 问题:$dp[i][j] = max \lbrace dp[i + 1][j - 1], \quad dp[i + 1][j], \quad dp[i][j - 1] \rbrace + cost[i][j], \quad i \le j$
- 枚举区间的起点;
- 枚举区间的终点;
- 根据状态转移方程计算从小区间转移到更大区间后的最优值。
- 多个(大于等于2个)小区间转移到大区间的区间 DP 问题:$dp[i][j] = max / min \lbrace dp[i][k] + dp[k + 1][j] + cost[i][j] \rbrace, \quad i < k \le j$
- 枚举区间长度;
- 枚举区间的起点,根据区间起点和区间长度得出区间终点;
- 枚举区间的分割点,根据状态转移方程计算合并区间后的最优值。
分析
- 划分阶段:按照区间长度进行阶段划分。
- 定义状态:dp[i][j]表示s在[i,j]范围内的最长回文子序列长度。
- 状态转移方程:$dp[i][j] = \begin{cases} max \lbrace dp[i + 1][j - 1] + 2 \rbrace & s[i] = s[j] \cr max \lbrace dp[i][j - 1], dp[i - 1][j] \rbrace & s[i] \ne s[j] \end{cases}$
- 初始条件:单个字符的最长回文序列是1,
dp[i][i] = 1
- 返回结果:
dp[i][j]依赖于dp[i+1][j-1]、dp[i+1][j]和dp[i][j-1],所以i应该从n-1到0枚举,而j应该从i+1到n-1枚举。所以最终应该返回dp[0][n-1]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public:
int longestPalindromeSubseq(string s) {
int n = s.length();
vector<vector<int>> dp(n, vector<int>(n));
for(int i = 0; i < n; i++){
dp[i][i] = 1;
}
for(int i = n-1; i >= 0; i--){
for(int j = i+1; j < n; j++){
if(s[i] == s[j]){
dp[i][j] = dp[i+1][j-1] + 2;
}
else{
dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
}
}
}
return dp[0][n-1];
}
};
|
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n^2)$
分析
在首尾加上两个气球,金币数为1,方便计算。
- 划分阶段:按照区间长度进行阶段划分。
- 定义状态:dp[i][j]表示戳破所有(i,j)之间的气球所获得的最大金币数。
- 状态转移方程:假设气球i与气球j之间最后一个被戳破的气球编号为
dp[i][j] = dp[i][k] + dp[k][j] + cost(k),cost(k) = max(nums[i] × nums[k] × nums[j]), i < k < j。
- 初始条件:dp[i][j]表示的是开区间,则
i < j-1,当i >= j-1, dp[i][j] = 0。
- 返回结果:dp[0][n+1]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public:
int maxCoins(vector<int>& nums) {
int n = nums.size();
vector<int> arr(n + 2);
arr[0] = 1;
arr[n+1] = 1;
for(int i = 1; i <= n; i++){
arr[i] = nums[i-1];
}
vector<vector<int>> dp(n+2, vector<int>(n+2));
for(int len = 3; len <= n+2; len++){
for(int i = 0; i < n+2; i++){
int j = i + len - 1;
if(j >= n + 2){
break;
}
for(int k = i + 1; k <= j-1; k++){
dp[i][j] = max(dp[i][j], dp[i][k] + dp[k][j] + arr[i] * arr[k] * arr[j]);
}
}
}
return dp[0][n+1];
}
};
|
- 时间复杂度:$O(n^3)$
- 空间复杂度:$O(n^2)$
分析
在数组中添加0和n并进行排序,形成区间。
- 划分阶段:按照区间长度进行阶段划分。
- 定义状态:dp[i][j]表示切割[i,j]上的小木棍的最小成本。
- 状态转移方程:$dp[i][j] = min \lbrace dp[i][k] + dp[k][j] + cuts[j] - cuts[i] \rbrace, \quad i < k < j$
- 初始条件:相邻位置之间没有切割点,不需要切割,最小成本为0,即dp[i-1][i]=0。其余位置默认为最小成本为一个极大值。
- 返回结果:dp[0][n-1]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public:
int minCost(int n, vector<int>& cuts) {
cuts.push_back(0);
cuts.push_back(n);
sort(cuts.begin(), cuts.end());
int size = cuts.size();
vector<vector<int>> dp(size, vector<int>(size));
for(int i = 1; i < size; i++){
dp[i-1][i] = 0;
}
for(int len = 3; len <= size; len++){
for(int i = 0; i < size; i++){
int j = i + len - 1;
if(j >= size){
break;
}
dp[i][j] = INT_MAX;
for(int k = i+1; k < j; k++){
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + cuts[j] - cuts[i]);
}
}
}
return dp[0][size-1];
}
};
|
- 时间复杂度:$O(n^3)$
- 空间复杂度:$O(n^2)$
分析
之前都是用双指针的方法做的,根据上面学习的内容,再来用动态规划做一遍。
- 划分阶段:按照区间长度进行阶段划分。
- 定义状态:dp[i][j]表示s[i:j]是否是回文的。
- 状态转移方程:$s[i] = s[j], dp[i][j] = \begin{cases} true & j-i \leq 2 \cr dp[i+1][j - 1] & else \end{cases}$
- 初始条件:dp[i][j]=false.
- 返回结果:s[maxStart:maxStart+maxLen]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public:
string longestPalindrome(string s) {
int n = s.length();
if(n == 1){
return s;
}
vector<vector<bool>> dp(n, vector<bool>(n));
int maxStart = 0;
int maxLen = 1;
for(int j = 1; j < n; j++){
for(int i = 0; i < j; i++){
if(s[i] == s[j]){
if(j - i <= 2){
dp[i][j] = true;
}
else{
dp[i][j] = dp[i+1][j-1];
}
}
if(dp[i][j] && j - i + 1 > maxLen){
maxLen = j - i + 1;
maxStart = i;
}
}
}
return s.substr(maxStart, maxLen);
}
};
|
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n^2)$
分析
- 划分阶段:按照区间长度进行阶段划分。
- 定义状态:dp[i][j]表示玩家1和玩家2在nums[i]…nums[j]之间选取,玩家1比玩家2多的最大分数。
- 状态转移方程:$dp[i][j] = \begin{cases}
nums[i] & i == j \cr \max \lbrace nums[i]-dp[i+1][j], nums[j]-dp[i][j-1] \rbrace & i \neq j
\end{cases}$
- 初始条件:如果
i == j,dp[i][j] = nums[i]
- 返回结果:dp[0][n-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
bool predictTheWinner(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> dp(n, vector<int>(n));
for(int len = 1; len <= n; len++){
for(int i = 0; i < n; i++){
int j = i + len - 1;
if(j >= n){
break;
}
if(len == 1){
dp[i][j] = nums[i];
}
else{
dp[i][j] = max(nums[i]-dp[i+1][j], nums[j]-dp[i][j-1]);
}
}
}
return dp[0][n-1] >= 0;
}
};
|
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n^2)$
分析
- 划分阶段:按照区间长度进行阶段划分。
- 定义状态:dp[i][j]表示打印i…j之间字符所需要的最少操作次数。
- 状态转移方程:$dp[i][j] = \begin{cases}
1 & i == k \cr dp[i][j-1] & s[i] == s[j] \cr \min \lbrace dp[i][k] + dp[k+1][j] \rbrace & s[i] \neq s[j], i < k < j
\end{cases}$
- 初始条件:如果
i == j,则dp[i][j] = 1,否则初始化为INT_MAX.
- 返回结果:dp[0][n-1]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public:
int strangePrinter(string s) {
int n = s.length();
vector<vector<int>> dp(n, vector<int>(n));
for(int i = 0; i < n; i++){
dp[i][i] = 1;
}
for(int len = 2; len <= n; len++){
for(int i = 0; i < n; i++){
int j = i + len - 1;
if(j >= n){
break;
}
dp[i][j] = 100;
if(s[i] == s[j]){
dp[i][j] = dp[i][j-1];
continue;
}
for(int k = i; k < j; k++){
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j]);
}
}
}
return dp[0][n-1];
}
};
|
- 时间复杂度:$O(n^3)$
- 空间复杂度:$O(n^2)$
动态规划+前缀和
先将无法将所有的石头合并成一堆的情况排除出去:每次将k堆合并成1堆,堆数会减少k-1堆。当$(n-1) \bmod (k-1) == 0$,说明可以将所有的石头合并成一堆,否则不能。
使用前缀和的方法计算出前i堆石头成本。
- 划分阶段:按照区间长度划分。
- 定义状态:dp[i][j][m]表示将区间[i,j]的石堆合并成m堆需要的最少成本,m取值为[1,k]。
- 状态转移方程:
- 先合并成m堆石头,$dp[i][j][m] = min_{i \le n < j} \lbrace dp[i][n][1] + dp[n + 1][j][m - 1] \rbrace$。
- 再合并成一堆:$dp[i][j][1] = dp[i][j][k] + \sum_{t = i}^{t = j} stones[t]$
- 初始条件:
dp[i][i][1] = 0
- 返回结果:
dp[0][size-1][1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| class Solution {
public:
int mergeStones(vector<int>& stones, int k) {
int size = stones.size();
if((size-1) % (k-1) != 0){
return -1;
}
vector<int> prefix(size + 1);
for(int i = 1; i <= size; i++){
prefix[i] = prefix[i-1] + stones[i-1];
}
vector<vector<vector<int>>> dp(size, vector<vector<int>>(size, vector<int>(k+1, 10000000)));
for(int i = 0; i < size; i++){
dp[i][i][1] = 0;
}
for(int len = 2; len <= size; len++){
for(int i = 0; i < size; i++){
int j = i + len - 1;
if(j >= size){
break;
}
for(int m = 2; m <= k; m++){
for(int n = i; n < j; n += k-1){
dp[i][j][m] = min(dp[i][j][m], dp[i][n][1] + dp[n+1][j][m-1]);
}
}
dp[i][j][1] = dp[i][j][k] + prefix[j+1] - prefix[i];
}
}
return dp[0][size-1][1];
}
};
|
- 时间复杂度:$O(n^3 \times k)$
- 空间复杂度:$O(n^2 \times k)$
动态规划 + 状态优化
上一种思路中,dp[i][j][m]表示将[i,j]区间的石头合并成m堆,m的取值为[1,k]。初始时,[i,j]内的堆数为j-i+1堆,每次合并都会减少k-1堆,合并到无法合并时的堆数固定为$(j-i) \bmod (k-1) + 1$,因此定义dp[i][j]为合并到无法合并时的最低成本。
- 划分阶段:按照区间长度进行阶段划分。
- 定义状态:dp[i][j]为合并到无法合并时的最低成本。
- 状态转移方程:枚举n,将区间[i,j]拆分成[i,n]和[n+1,j]两个区间,$dp[i][j] = min_{i \le n < j} \lBrace dp[i][n] + dp[n+1][j] \rBrace$,如果$(j-i) \bmod (k-1) == 0$,说明区间可以合并成一堆,
dp[i][j] += prefix[j+1] - prefix[i]
- 初始条件:长度为1的区间合并到无法合并时的最低成本为0,
dp[i][i] = 0
- 返回结果:dp[0][size-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class Solution {
public:
int mergeStones(vector<int>& stones, int k) {
int size = stones.size();
if((size-1) % (k-1) != 0){
return -1;
}
vector<int> prefix(size + 1);
for(int i = 1; i <= size; i++){
prefix[i] = prefix[i-1] + stones[i-1];
}
vector<vector<int>> dp(size, vector<int>(size, 10000000));
for(int i = 0; i < size; i++){
dp[i][i] = 0;
}
for(int len = 2; len <= size; len++){
for(int i = 0; i < size; i++){
int j = i + len -1;
if(j >= size){
break;
}
for(int n = i; n < j; n+=k-1){
dp[i][j] = min(dp[i][j], dp[i][n] + dp[n+1][j]);
}
if((j-i) % (k-1) == 0){
dp[i][j] += prefix[j+1] - prefix[i];
}
}
}
return dp[0][size-1];
}
};
|
- 时间复杂度:$O(n^3)$
- 空间复杂度:$O(n^2)$
区间DP剩余题目
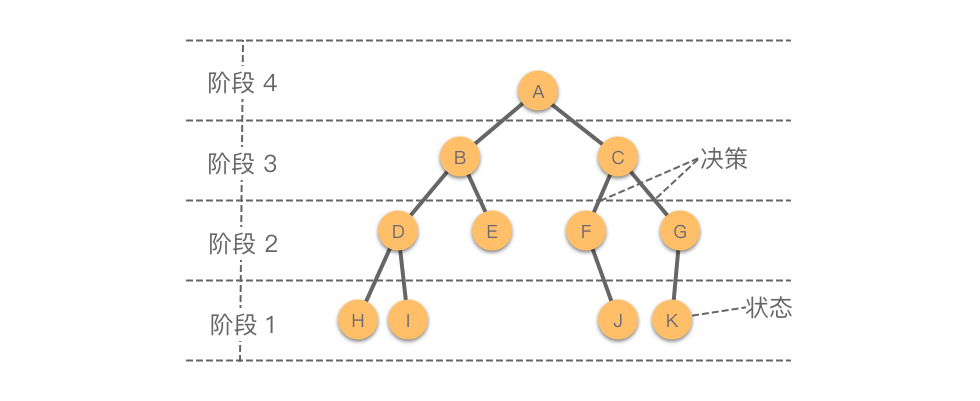
固定根的树形 DP 问题,如果是二叉树,树通常是以根节点的形式给出。我们可以直接从指定根节点出发进行深度优先搜索。如果是多叉树,树是以一张n个节点、n - 1条边的无向图形式给出的,并且事先给出指定根节点的编号。这种情况下,我们要先用邻接表存储下这n个点和n-1条边,然后从指定根节点出发进行深度优先搜索,并注意标记节点是否已经被访问过,以避免在遍历中沿着反向边回到父节点。
分析
该二叉树的最大路径和 = max(左子树中最大贡献值 + 右子树中最大贡献值 + 当前节点值,所有子树中最大路径和)。这道题在学递归算法的时候做过,再做一遍加深印象。
分析
最长路径长度 = max(某子树中的最长路径长度 + 另一子树中的最长路径长度 + 1,某个子树中的最长路径长度)。
- 先计算出从相邻节点v出发的最长路径长度vLen。
- 更新维护全局最长路径长度为
res = max(res, uLen + vLen + 1)
- 更新维护当前节点最长路径长度
uLen = max(uLen, vLen + 1)
因为题目限定了「相邻节点字符不同」,所以在更新全局最长路径长度和当前节点u的最长路径长度时,我们需要判断一下节点
u与相邻节点v的字符是否相同,只有在字符不同的条件下,才能够更新维护。
题目要求的是树的直径(树的最长路径长度)中的节点个数,节点个数=路径长度+1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
int res = 0;
int longestPath(vector<int>& parent, string s) {
int n = parent.size();
vector<vector<int>> graph(n);
for(int i = 1; i < n; i++){
graph[parent[i]].push_back(i);
}
dfs(0, graph, s);
return res + 1;
}
int dfs(int u, vector<vector<int>>& graph, string& s){
int uLen = 0;
for(int v : graph[u]){
int vLen = dfs(v, graph, s);
if(s[u] != s[v]){
res = max(res, uLen + vLen + 1);
uLen = max(uLen, vLen + 1);
}
}
return uLen;
}
};
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
[!NOTE]
在函数参数中传值和传引用有很大的区别,在这道题中,如果dfs函数按值传递,即dfs(string s)会超出内存限制,这是因为每次递归调用时都要复制字符串。而传引用,即dfs(string& s)可以节省大量内存,特别是当字符串比较长时。
「两次扫描与换根法」:
- 第一次扫描时,任选一个节点为根,在「有固定根的树」上执行一次树形 DP,预处理树的一些相关信息。
- 第二次扫描时,从刚才的根节点出发,对整棵树再执行一次深度优先搜索,同时携带根节点的一些信息提供给子节点进行推导,计算出「换根」之后的解。
分析
- 图的构建:用邻接表graph存储每个节点的邻居节点。
- 自底向上DFS,计算每个节点向下的最长路径:
- dfs函数实现了一次深度优先搜索(DFS),用于从叶子节点开始向上收集信息,即从子节点往父节点传递最长路径信息。
- 定义两个数组down1和down2,分别记录从每个节点出发向下走的最长路径和次长路径。
- 通过比较每个子节点的高度(即down1[v] + 1),更新当前节点的down1和down2,即节点向下走的最长路径和次长路径。同时,用p[u]记录下这个最长路径是由哪个子节点传上来的。
- 自顶向下DFS,计算每个节点向上的最长路径:
- 完成自底向上的DFS后,接着要计算每个节点向上的最长路径,即如果该节点作为根节点,其向父节点方向可以走多远。定义一个数组up来记录这一信息。
- reroot函数实现自顶向下的动态规划。对于每个节点u的每个子节点v:
- 如果v是当前节点u的最长路径的子节点(即p[u] == v),则up[v]从u向上走的最长路径要结合down2[u](次长路径)来计算。
- 如果v不是最长路径的子节点,up[v]从u向上走的路径可以结合down1[u](最长路径)来计算。
- 计算每个节点的最大高度:
- 对于每个节点,树的高度就是它的最大高度,也就是它向下的最长路径down1[i]和向上的最长路径up[i]的最大值。
- 找到所有节点中具有最小高度的那些节点。
- 最后,将所有具有最小高度的节点放入结果数组中并返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
| class Solution {
public:
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
vector<vector<int>> graph(n);
for(auto& edge : edges){
int u = edge[0];
int v = edge[1];
graph[u].push_back(v);
graph[v].push_back(u);
}
vector<int> down1(n);
vector<int> down2(n);
vector<int> p(n);
function<void(int, int)> dfs = [&](int u, int fa){
for(int v : graph[u]){
if(v == fa){
continue;
}
dfs(v, u);
int height = down1[v] + 1;
if(height > down1[u]){
down2[u] = down1[u];
down1[u] = height;
p[u] = v;
}
else if(height > down2[u]){
down2[u] = height;
}
}
};
vector<int> up(n);
function<void(int,int)> reroot = [&](int u, int fa){
for(int v : graph[u]){
if(v == fa){
continue;
}
if(p[u] == v){
up[v] = max(up[u], down2[u]) + 1;
}
else{
up[v] = max(up[u], down1[u]) + 1;
}
reroot(v, u);
}
};
dfs(0, -1);
reroot(0, -1);
int minHeight = INT_MAX;
for(int i = 0; i < n; i++){
minHeight = min(minHeight, max(down1[i], up[i]));
}
vector<int> res;
for(int i = 0; i < n; i++){
int h = max(down1[i], up[i]);
if(h == minHeight){
res.push_back(i);
}
}
return res;
}
};
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
[!WARNING]
这道题按照给的步骤思路写出来了,但是不是特别懂,以后再看看。
练习题目
分析
二叉树的直径 = max(左子树高度+右子树高度,所有子树最大直径长度)。
在递归遍历左子树时,如果当前节点与左子树的值相同,则:$\text{包含当前节点向左的最长同值路径长度} = \text{左子树最长同值路径长度} + 1$,否则为 0。
在递归遍历左子树时,如果当前节点与左子树的值相同,则:$\text{包含当前节点向右的最长同值路径长度} = \text{右子树最长同值路径长度} + 1$,否则为0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public:
int res = 0;
int longestUnivaluePath(TreeNode* root) {
dfs(root);
return res;
}
int dfs(TreeNode* root){
if(!root){
return 0;
}
int leftLen = dfs(root->left);
int rightLen = dfs(root->right);
if(root->left && root->left->val == root->val){
leftLen++;
}
else{
leftLen = 0;
}
if(root->right && root->right->val == root->val){
rightLen++;
}
else{
rightLen = 0;
}
res = max(res, leftLen + rightLen);
return max(leftLen, rightLen);
}
};
|
- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
分析
- 通过二进制枚举的方式,得到所有子树。
- 对于当前子树,通过树形 DP + 深度优先搜索的方式,计算出当前子树的直径。
- 统计所有子树直径中经过的不同边数个数,将其放入答案数组中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| class Solution {
public:
vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {
vector<vector<int>> graph(n);
for(auto& edge : edges){
int u = edge[0] - 1;
int v = edge[1] - 1;
graph[u].push_back(v);
graph[v].push_back(u);
}
int visited = 0, diameter = 0;
vector<int> ans(n - 1, 0);
function<int(int, int)> dfs = [&](int mask, int u) -> int{
visited |= (1 << u);
int uLen = 0;
for(int v : graph[u]){
if(((visited >> v) & 1) == 0 && ((mask >> v) & 1)){
int vLen = dfs(mask, v);
diameter = max(diameter, uLen + vLen + 1);
uLen = max(uLen, vLen + 1);
}
}
return uLen;
};
for(int mask = 3; mask < (1 << n); mask++){
if(__builtin_popcount(mask) <= 1){
continue;
}
visited = 0;
diameter = 0;
int u = 31 - __builtin_clz(mask);
dfs(mask, u);
if (visited == mask){
ans[diameter-1]++;
}
}
return ans;
}
};
|
- 时间复杂度:$O(n \times 2^n)$
- 空间复杂度:$O(n)$
分析
第一次遍历:从编号为0的根节点开始,自底向上地计算出节点0到其他的距离之和,记录在 res[0]中。并且统计出以子节点为根节点的子树节点个数size[v]。
第二次遍历:从编号为0的根节点开始,自顶向下地枚举每个点,计算出将每个点作为新的根节点时,其他节点到根节点的距离之和。如果当前节点为v,其父节点为u,则自顶向下计算出res[u]后,将根节点从u换为节点v,子树上的点到新根节点的距离比原来都小了1,非子树上剩下所有点到新根节点的距离比原来都大了1。则可以据此计算出节点v与其他节点的距离和为:$res[v] = res[u] + n - 2 \times sizes[u]$。
