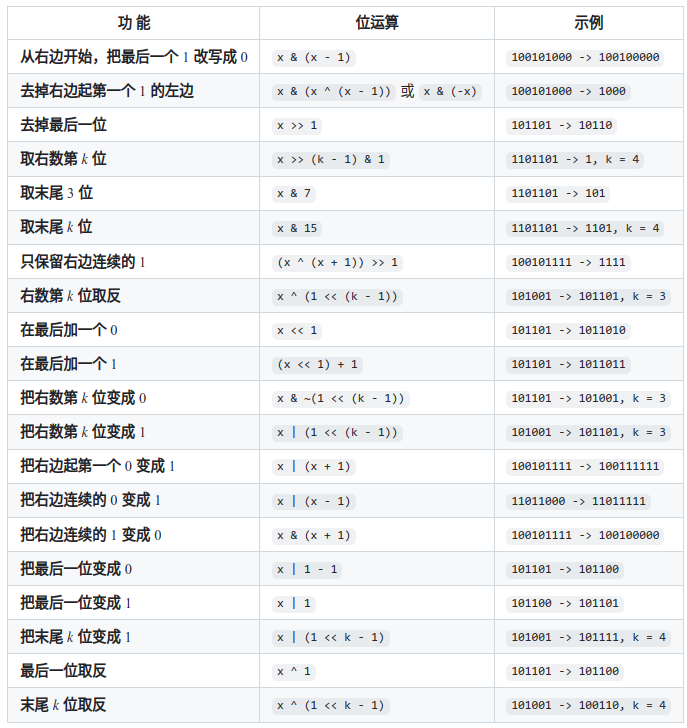
0405位运算

04.05 位运算

位运算

常用操作

判断整数奇偶

通过与1进行按位与运算，即可判断某个数是奇数还是偶数。

  • (x & 1) == 0 为偶数。
  • (x & 1) == 1 为奇数。

二进制数选取指定位

如果我们想要从一个二进制数X中取出某几位，使取出位置上的二进位保留原值，其余位置为0，则可以使用另一个二进制数Y，使该二进制数上对应取出位置为 1
，其余位置为0。然后令两个数进行按位与运算（X & Y），即可得到想要的数。

将指定位设置为1

按位或运算可以实现，要保持原值的为0，要变成1的位置为1。

反转指定位

如果我们想要把一个二进制数X的某几位进行反转，则可以使用另一个二进制数Y，使得该二进制上对应选取位置为 1，其余位置为 0。然后令两个数进行按位异或运算。

交换两个数

通过按位异或运算可以实现交换两个数的目的（只能用于交换两个整数）。

1
2
3
4
5
a, b = 10, 20
a ^= b
b ^= a
a ^= b
print(a, b)

将二进制最右侧为1的二进位改为0

如果我们想要将一个二进制数最右侧为1的二进制位X改为 0，则只需通过 X & (X - 1) 的操作即可完成。

计算二进制中二进位为1的个数

通过 X & (X - 1) 我们可以将二进制X最右侧为1的二进制位改为 0，那么如果我们不断通过 X & (X - 1) 操作，最终将二进制X变为0，并统计执行次数，则可以得到二进制中二进位为1的个数。

判断某数是否为2的幂次方

通过判断 X & (X - 1) == 0 是否成立，即可判断x
是否为2的幂次方。

常用操作总结

颠倒二进制位

分析

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    uint32_t reverseBits(uint32_t n) {
        int res = 0;
        for(int i = 0; i < 32; i++){
            res = (res << 1) | (n & 1);
            n >>= 1;
        }
        return res;
    }
};
  • 时间复杂度：O(1)
  • 空间复杂度：O(1)

位1的个数

分析

不断通过 X & (X - 1) 操作，最终将二进制X变为0，并统计执行次数，则可以得到二进制中二进位为1的个数。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int hammingWeight(int n) {
        int res = 0;
        while(n){
            n = n & (n-1);
            res++;
        }
        return res;
    }
};
  • 时间复杂度：$O(\log n)$。
  • 空间复杂度：O(1)

数字范围按位与

分析

按位与

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int rangeBitwiseAnd(int left, int right) {
        while(left < right){
            right = right & (right-1);
        }
        return right;
    }
};
  • 时间复杂度：O(logn)
  • 空间复杂度：O(1)

https://github.com/datawhalechina/leetcode-notes/blob/main/docs/ch04/04.05/04.05.03-Exercises.md

只出现一次的数字

分析

两个相同的数字做异或运算，得到的是全0，所以只出现一次的数字最后会和全0异或，得到它本身。

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int res = nums[0];
        for(int i = 1; i < nums.size(); i++){
            res ^= nums[i];
        }
        return res;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

只出现一次的数字II

分析

将出现三次的元素换成二进制形式放在一起，其二进制对应位置上，出现 1的个数一定是3的倍数（包括0）。此时，如果在放进来只出现一次的元素，则某些二进制位置上出现1的个数就不是3的倍数了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int res = 0;
        for(int i = 0; i < 32; i++){
            int cnt = 0;
            for(int j = 0; j < nums.size(); j++){
                cnt += (nums[j] >> i) & 1;
            }
            if(cnt % 3 != 0){
                res = res | (1 << i);
            }
        }
        return res;
    }
};
  • 时间复杂度：O(nlogm)，本题中$logm = log2^{32}$
  • 空间复杂度：O(1)

只出现一次的数字III

分析

  1. 求所有数字的异或值：如果数组中有两个数字只出现一次，其余每个元素均出现两次。那么经过全部异或运算。我们可以得到只出现一次的两个数字的异或结果。
  2. 找到最低的不同位。
  3. 根据最低不同位分组：
    • 根据 mask 的位置，将数组中的数字分为两组：一组在 mask 位置上为 0，另一组在 mask 位置上为 1。
    • 因为相同的数字会被分到同一组且异或为0，最终每组剩下的数字就是 a 和 b。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        // 得到异或结果
        int all = nums[0];
        for(int i = 1; i <nums.size(); i++){
            all ^= nums[i];
        }
        // 找到最低位为1的位置，即最低位的两个数字不相同的位
        int mask = 1;
        while((all & mask) == 0){
            mask <<= 1;
        }
        // 分组
        int a = 0, b = 0;
        for(int i = 0; i < nums.size(); i++){
            if((mask & nums[i]) == 0){
                a ^= nums[i];
            }
            else{
                b ^= nums[i];
            }
        }
        return {a, b};
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

注：运算符 & 的优先级低于 ==。

七进制数

分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    string convertToBase7(int num) {
        string res;
        int quotient = abs(num / 7);
        int remainder = abs(num % 7);
        while(quotient){
            res += to_string(remainder);
            remainder = quotient % 7;
            quotient /= 7;
        }
        res += to_string(remainder);
        reverse(res.begin(), res.end());
        return num < 0 ? "-" + res : res;
    }
};
  • 时间复杂度：$O(\log |n|)$。
  • 空间复杂度：$O(\log |n|)$。

数字转换为十六进制数

分析

  • 当x为0，直接返回0.
  • 当x>0，不断做除以16取余的运算。
  • 当x<0，进行补码运算，即每一位取反+1（也相当于与全1异或再加1，1与1异或是0，0与1异或是1），再按照正数运算。
  • 最后逆转字符串。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    string toHex(int num) {
        if(num == 0){
            return "0";
        }
        // 使用无符号整数表示补码
        unsigned int n = static_cast<unsigned int>(num);
        
        // 不断取余
        string res;
        int remainder;
        while(n) {
            remainder = n % 16;
            n /= 16;
            if(remainder < 10){
                res += to_string(remainder);
            }
            else{
                res += static_cast<char>(remainder - 10 + 'a');
            }
        }
        reverse(res.begin(), res.end());
        return res;
    }
};

  • 时间复杂度：O(k)，k是整数的十六进制数的位数。
  • 空间复杂度：O(k)。

[!NOTE]
static_cast

十进制整数的反码

分析

确定输入数字的二进制表示的有效位数,只对有效位数进行反码操作。

  • 找到 n 的二进制有效位数。
  • 构造一个与 n 有相同位数且每一位都是 1 的掩码(mask)。
  • 对 n 进行按位异或操作，得到不含前导 0 的反码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int bitwiseComplement(int n) {
        // 特殊情况，0 的反码是 1
        if (n == 0) return 1;

        // 找到 n 的二进制表示的最高位
        int mask = 0;
        int temp = n;
        while (temp > 0) {
            mask = (mask << 1) | 1;
            temp >>= 1;
        }

        // 按位取反：使用 n 与 mask 进行按位异或
        return n ^ mask;
    }
};
  • 时间复杂度：O(k)，k为有效二进制位数。
  • 空间复杂度：O(1)

两整数之和

分析

使用异或运算，同时标记进位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int getSum(int a, int b) {
        while(b){
            // 计算进位
            int carry = a & b;
            // 计算和
            a ^= b;
            // 将进位移动到正确的位置
            b = carry << 1;
        }
        return a;
    }
};
  • 时间复杂度：O(log(max_int))
  • 空间复杂度：O(1)

比特位计数

分析

直接位运算+暴力。题解中还有动态规划等等的方法，以后刷到动态规划再来看。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> countBits(int n) {
        vector<int> res;
        for(int i = 0; i <= n; i++){
            res.push_back(count(i));
        }
        return res;
    }
    int count(int x){
        int cnt = 0;
        while(x){
            x = x & (x-1);
            cnt++;
        }
        return cnt;
    }
};
  • 时间复杂度：$O(nlogn)$
  • 空间复杂度：O(1)

丢失的数字

分析

考虑两个相同的数字异或，得到0。先得到数组中所有数字异或的结果，再与0~n异或，即把题目转换为只出现一次的数字。

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int res = 0;
        for(int i = 0; i < nums.size(); i++){
            res ^= nums[i] ^ (i+1);
        }
        return res;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

格雷编码

参加考试的最大学生数

错误的集合

子集

子集II

算法笔记 > 贪心
#leetcode-notes
0405位运算
http://example.com/2024/09/19/posts/0405位运算/
作者
Xuan Yang
发布于
2024年9月19日
许可协议