0403回溯算法

04.03 回溯算法

一种能避免不必要搜索的穷举式的搜索算法。采用试错的思想，在搜索尝试过程中寻找问题的解，当探索到某一步时，发现原先的选择并不满足求解条件，或者还需要满足更多求解条件时，就退回一步（回溯）重新选择，这种走不通就退回再走的技术称为「回溯法」，而满足回溯条件的某个状态的点称为「回溯点」。

  1. 明确所有选择：画出搜索过程的决策树，根据决策树来确定搜索路径。
  2. 明确终止条件：推敲出递归的终止条件，以及递归终止时的要执行的处理方法。
  3. 将决策树和终止条件翻译成代码：
  • 定义回溯函数（明确函数意义、传入参数、返回结果等）。
  • 书写回溯函数主体（给出约束条件、选择元素、递归搜索、撤销选择部分）。
  • 明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。

子集

分析

  1. 明确所有选择：根据数组中每个位置上的元素选与不选两种选择，画出决策树。
  2. 明确终止条件：当遍历到决策树的叶子节点时，就终止了。即当前路径搜索到末尾时，递归终止。
  3. 将决策树和终止条件翻译成代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;
        vector<int> path;
        helper(nums, 0, path, res);
        return res;
    }
    // 回溯法
    void helper(vector<int>& nums, int index, vector<int>& path,vector<vector<int>>& res){
        // 递归结束
        if(index == nums.size()){
            res.push_back(path);
            return;
        }
        // 不加入当前数字
        helper(nums, index+1, path, res);
        // 加入当前数字
        path.push_back(nums[index]);
        helper(nums, index+1, path, res);
        path.pop_back();
    }
};

之前在LCR079中做过这道题，当时分析的时间复杂度是$O(2^n)$，但是官方题解中给出的时间复杂度是$O(n \cdot{2^n})$，查了一下剑指offer书中的不够准确。每个递归分支都会生成一个子集，总共有$2^n$个子集，对于每个子集生成过程最多需要$O(n)$的时间。

  • 时间复杂度：$O(n \cdot 2^n)$
  • 空间复杂度：leetcode官方题解中在分析空间复杂度时，一般不考虑返回的结果所占用的空间，但是chatgpt说需要考虑结果所占用的空间。代码随想录给出的解释是

    $O(n)$，递归深度为n，所以系统栈所用空间为$O(n)$，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为$O(n)$。

N皇后

分析

  1. 明确所有选择：根据棋盘中当前行的所有列位置上是否选择放置皇后，画出决策树。
  2. 明确终止条件：当遍历到决策树的叶子节点时，就终止了。也就是在最后一行放置完皇后时，递归终止。
  3. 将决策树和终止条件翻译成代码：
    翻译代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
public:
    vector<vector<string>> res;
    vector<vector<string>> solveNQueens(int n) {
        // 定义棋盘
        vector<string> chessBoard(n, string(n, '.'));
        // 回溯搜索
        backtrack(chessBoard, 0);
        return res;
    }
    // row 是当前递归到棋盘的第几行
    void backtrack(vector<string>& chessBoard, int row){
        // 搜索到叶子结点，结束
        if(row == chessBoard.size()){
            res.push_back(chessBoard);
            return;
        }
        // 逐列放置皇后
        for(int col = 0; col < chessBoard.size(); col++){
            // 验证合法，放置皇后
            if(isValid(chessBoard, row, col)){
                chessBoard[row][col] = 'Q';
                backtrack(chessBoard, row + 1);
                chessBoard[row][col] = '.';
            }
        }
    }
    bool isValid(vector<string>& chessBoard, int row, int col){
        // 判断这一列的每一行是否有皇后
        int n = chessBoard.size();
        for(int i = 0; i < row; i++){
            if(chessBoard[i][col] == 'Q'){
                return false;
            }
        }
        // 判断45度角方向
        for(int i = row-1, j = col-1; i >=0 && j >= 0; i--, j--){
            if(chessBoard[i][j] == 'Q'){
                return false;
            }
        }
        // 判断135度角方向
        for(int i = row-1, j = col+1; i >= 0 && j < n; i--, j++){
            if(chessBoard[i][j] == 'Q'){
                return false;
            }
        }
        return true;
    }
};

  • 时间复杂度：O(n!)，第一个皇后有 n 列可以选择，第二个皇后最多有 n−1 列可以选择，第三个皇后最多有 n−2 列可以选择（如果考虑到不能在同一条斜线上，可能的选择数量更少），因此所有可能的情况不会超过 n! 种。

  • 空间复杂度：O(n)

剩下的练习题目应该是在剑指offer里做过的，但是有点忘记了，再重新做一遍。

全排列

分析

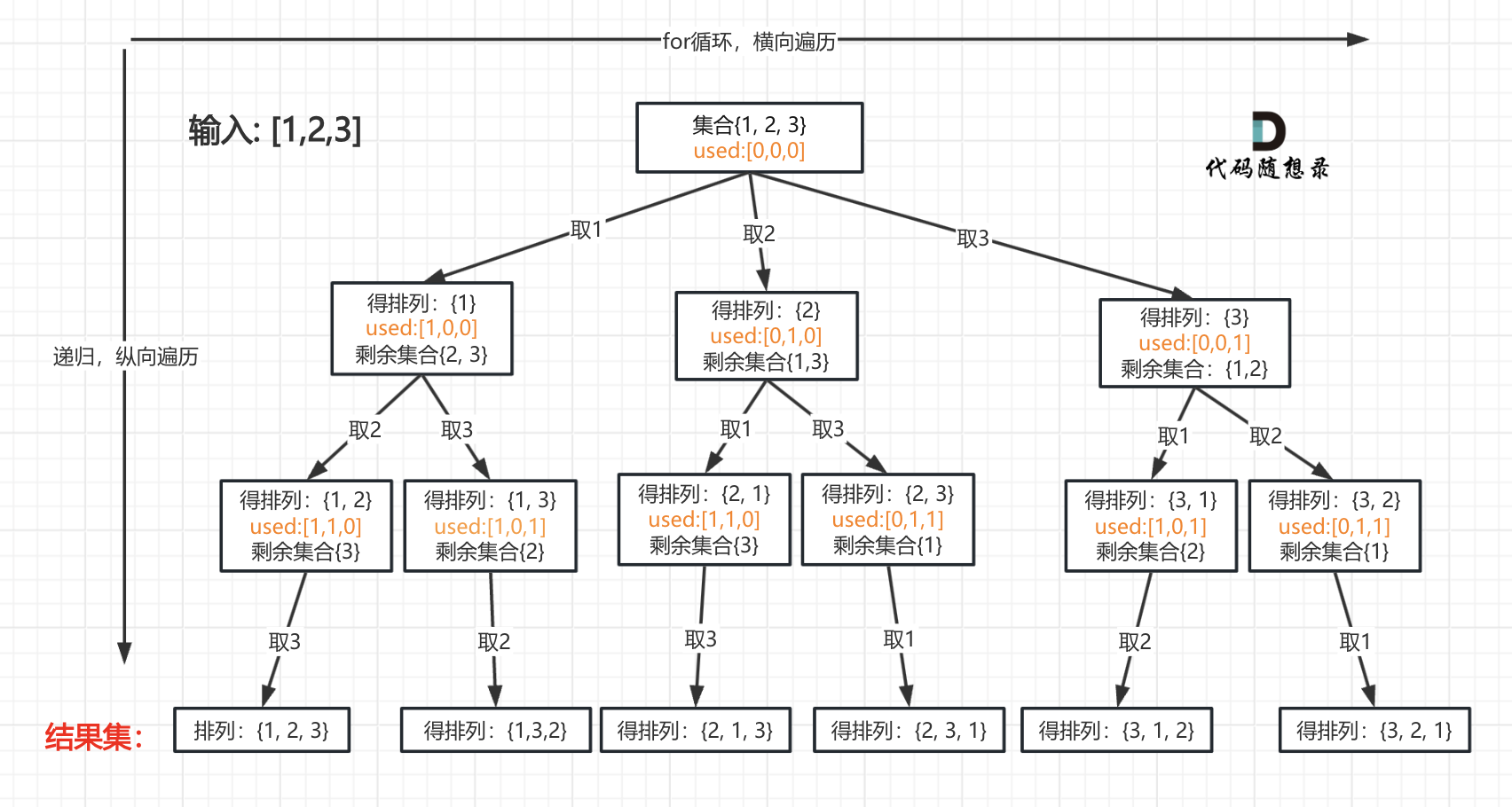
  1. 明确所有选择：全排列中每个位置上的元素都可以从剩余可选元素中选出，对此画出决策树。
    全排列决策树
  2. 明确终止条件：当遍历到决策树的叶子节点时，就终止了。即当前路径搜索到末尾时，递归终止。
  3. 将决策树和终止条件翻译成代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> res;
        helper(nums, 0, res);
        return res;
    }
    void helper(vector<int>& nums, int index, vector<vector<int>>& res){
        // 搜索结束
        if(index == nums.size()){
            res.push_back(nums);
            return;
        }
        for(int i = index; i < nums.size(); i++){
            swap(nums[i], nums[index]);
            helper(nums, index+1, res);
            swap(nums[i], nums[index]);
        }
    }
};
  • 时间复杂度：O(n!)
  • 空间复杂度：O(n)

全排列II

分析

和上一题的区别是，nums中可能包含重复的元素，但返回得结果不能有两个一样的排列。用unordered_set保存已经访问过的数字，后面如果再遇到，可以直接不处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> res;
        helper(nums, 0, res);
        return res;
    }
    void helper(vector<int>& nums, int index, vector<vector<int>>& res){
        // 递归结束
        if(index == nums.size()){
            res.push_back(nums);
            return;
        }
        // 定义一个集合用于存放当前位置已经使用过的元素
        unordered_set<int> set;
        for(int i = index; i < nums.size(); i++){
            if(set.find(nums[i]) == set.end()){
                set.insert(nums[i]);
                swap(nums[i], nums[index]);
                helper(nums, index+1, res);
                swap(nums[i], nums[index]);
            }
        }
    }
};
  • 时间复杂度：O(n!)
  • 空间复杂度：O(n)

这两道题的复杂度分析和之前做的又不一样。各个资料的分析都不太一样，但是都有一定的道理……以后再回来看看。

括号生成

分析

  1. 明确所有选择：$2 \times n$ 的括号组合中的每个位置，都可以从 ( 或者 ) 中选出。并且，只有在 symbol < n 的时候，才能选择 (，在 symbol > 0 的时候，才能选择 )。
  2. 明确终止条件：当遍历到决策树的叶子节点时，就终止了。即当前路径搜索到末尾时，递归终止。
  3. 传入参数：左括号剩余数，右括号剩余数，当前字符串，结果。递归结束条件：左括号右括号剩余数等于0。条件选择：left>0选择左括号；left < right选择右括号，因为当left==right时，不能再选择右括号。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<string> generateParenthesis(int n) {
        string s;
        vector<string> res;
        helper(n, n, s, res);
        return res;
    }
    void helper(int left, int right, string s, vector<string>& res){
        // 递归结束
        if(left == 0 && right == 0){
            res.push_back(s);
            return;
        }
        // 选择左括号
        if(left > 0){
            helper(left-1, right, s + "(", res);
        }
        // 选择右括号
        if(left < right){
            helper(left, right-1, s + ")", res);
        }
    }
};
  • 时间复杂度：$\frac{4^n}{\sqrt{n}}$
  • 空间复杂度：O(n)

电话号码的字母组合

分析

用哈希表保存每个数字键位对应的所有可能的字母，然后进行回溯操作。

回溯过程中，维护一个字符串 combination，表示当前的字母排列组合。初始字符串为空，每次取电话号码的一位数字，从哈希表中取出该数字所对应的所有字母，并将其中一个插入到 combination 后面，然后继续处理下一个数字，知道处理完所有数字，得到一个完整的字母排列。开始进行回退操作，遍历其余的字母排列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
private:
    unordered_map<char, string> hash = {{'2',"abc"}, {'3', "def"}, {'4',"ghi"}, {'5',"jkl"}, {'6',"mno"}, {'7',"pqrs"}, {'8',"tuv"}, {'9',"wxyz"}};

public:
    vector<string> letterCombinations(string digits) {
        if(digits.length() == 0){
            return {};
        }
        string combination;
        vector<string> res;
        backtrack(digits, 0, combination, res);
        return res;
    }
    void backtrack(string digits, int index, string& combination, vector<string>& res){
        // 递归结束
        if(index == digits.length()){
            res.push_back(combination);
            return;
        }
        // 对于每一个字符
        char digit = digits[index];
        for(int i = 0; i < hash[digit].length(); i++){
            char add = hash[digit][i];
            combination += add;
            backtrack(digits, index+1, combination, res);
            combination = combination.substr(0, combination.length()-1);
        }
    }
};

  • 时间复杂度：$O(3^m \times 4^n)$，其中 m 是输入中对应 3 个字母的数字个数（包括数字 2、3、4、5、6、8），n 是输入中对应 4 个字母的数字个数（包括数字 7、9），m+n 是输入数字的总个数。当输入包含 m 个对应 3 个字母的数字和 n 个对应 4 个字母的数字时，需要遍历每一种字母组合。

  • 空间复杂度：O(m+n)

组合总和

分析

递归结束条件：当前和等于target。

递归选择条件：选择当前元素/不选择当前元素。前提是选择后和不能大于target。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<int> path;
        vector<vector<int>> res;
        backtrack(candidates, target, 0, 0, path, res);
        return res;
    }
    void backtrack(vector<int>& candidates, int target, int index, int sum, vector<int>& path, vector<vector<int>>& res){
        // 递归结束
        if(sum == target){
            res.push_back(path);
            return;
        }
        if(index == candidates.size()){
            return;
        }

        // 选择当前元素
        if(sum + candidates[index] <= target){
            path.push_back(candidates[index]);
            backtrack(candidates, target, index, sum + candidates[index], path, res);
            path.pop_back();
        }
        // 不选择当前元素
        backtrack(candidates, target, index+1, sum, path, res);
    }
};
  • 时间复杂度：$O(2^n \times n)$
  • 空间复杂度：$O(target)$，递归函数需要用到栈空间，栈空间取决于递归深度。

组合总和II

分析

为了方便跳过后面所有值相同的数字，可以将集合中的所有数字排序，把相同的数字放在一起，这样方便比较数字。当决定跳过某个值的数字时，可以按顺序扫描后面的数字，直到找到不同的值为止。当决定跳过数字nums[i]时可以调用函数getNext找到与该数字不同的下一个数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        // 先进行排序
        sort(candidates.begin(), candidates.end());
        vector<int> path;
        vector<vector<int>> res;
        backtrack(candidates, target, 0, 0, path, res);
        return res;
    }
    void backtrack(vector<int>& candidates, int target, int index, int sum, vector<int>& path, vector<vector<int>>& res){
        // 递归结束
        if(sum == target){
            res.push_back(path);
            return;
        }
        if(index == candidates.size()){
            return;
        }
        // 不选择当前元素
        backtrack(candidates, target, getNext(candidates, index), sum, path, res);
        // 选择当前元素
        if(sum + candidates[index] <= target){
            path.push_back(candidates[index]);
            backtrack(candidates, target, index+1, sum+candidates[index], path, res);
            path.pop_back();
        }

    }
    // 获取下一个索引
    int getNext(vector<int>& candidates, int index){
        int next = index + 1;
        while(next < candidates.size() && candidates[next] == candidates[index]){
            next++;
        }
        return next;
    }
};
  • 时间复杂度：$O(n \times 2 ^ n)$
  • 空间复杂度：$O(n)$

子集II

分析

其中可能包含重复元素，可以考虑先进行排序，然后跳过该位置上相同的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        // 对数组进行排序
        sort(nums.begin(), nums.end());
        vector<int> path;
        vector<vector<int>> res;
        backtrack(nums, 0, path, res);
        return res;
    }
    void backtrack(vector<int>& nums, int index, vector<int>& path, vector<vector<int>>& res){
        // 递归结束
        if(index == nums.size()){
            res.push_back(path);
            return;
        }
        // 不选择当前元素
        backtrack(nums, getNext(nums, index), path, res);
        // 选择当前元素
        path.push_back(nums[index]);
        backtrack(nums, index + 1, path, res);
        path.pop_back();
    }
    int getNext(vector<int>& nums, int index){
        int next = index + 1;
        while(next < nums.size() && nums[next] == nums[index]){
            next++;
        }
        return next;
    }
};
  • 时间复杂度：$O(n \times 2 ^ n)$
  • 空间复杂度：O(n)

单词搜索

分析

设函数backtrack(i, j, index)表示从board[i][j]出发，能否搜索到字母word[index]，及其后续的子串。

三种情况：

  • board[i][j] == word[index] && index == word.length()-1，递归结束，返回true。
  • board[i][j] == word[index] && index < word.length()-1，向每个方向递归搜索，如果有返回true的，返回true，否则返回false。
  • board[i][j] != word[index]，返回false。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        int m = board.size();
        int n = board[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (backtrack(board, word, i, j, 0, visited)) {
                    return true;
                }
            }
        }
        return false;
    }
    
    bool backtrack(vector<vector<char>>& board, string& word, int i, int j, int index, vector<vector<bool>>& visited) {
        // 检查是否找到了整个单词
        if (index == word.length()) return true;
        
        // 检查边界条件和当前字符是否匹配
        if (i < 0 || i >= board.size() || j < 0 || j >= board[0].size() || 
            visited[i][j] || board[i][j] != word[index]) {
            return false;
        }
        
        // 标记当前位置为已访问
        visited[i][j] = true;
        
        // 向四个方向搜索
        bool result = backtrack(board, word, i+1, j, index+1, visited) ||
                      backtrack(board, word, i-1, j, index+1, visited) ||
                      backtrack(board, word, i, j+1, index+1, visited) ||
                      backtrack(board, word, i, j-1, index+1, visited);
        
        // 回溯，将当前位置标记为未访问
        visited[i][j] = false;
        
        return result;
    }
};
  • 时间复杂度：最坏情况下，我们需要遍历整个板子的每个位置作为起点。对于每个起点，我们可能需要探索所有可能的路径。假设板子的大小为 m × n，单词长度为 k。对于每个起点，在最坏情况下，我们可能需要探索 4^k 条路径（因为每一步有4个方向可以选择，总共k步）。因此，总的时间复杂度为$O(m n 4^k)$。
  • 空间复杂度：我们使用了一个 visited 数组，大小与板子相同，即 O(m n)。递归调用栈的深度最大为单词的长度 k。因此，总的空间复杂度为 O(mn + k)。

虽然理论上的最坏时间复杂度是 O(m n 4^k)，但在实际情况中，由于我们有提前终止的条件（如字符不匹配就返回），实际运行时间通常会好很多。

这个问题是NP完全问题，没有已知的多项式时间解法。当输入规模变大时，最坏情况下的时间复杂度会急剧增加。

在实际应用中，可以考虑一些优化策略，比如先检查板子中是否包含单词中的所有字符，如果不包含，可以直接返回false，避免不必要的搜索。

解数读

分析

对于每一行、每一列、每一个数字，都需要一重 for 循环来遍历，这样就是三重 for 循环。

对于第i行、第j列的元素来说，如果当前位置为空位，则尝试将第k个数字置于此处，并检验数独的有效性。如果有效，则继续遍历下一个空位，直到遍历完所有空位，得到可行方案或者遍历失败时结束。

遍历完下一个空位之后再将此位置进行回退，置为.。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {
        backtrack(board);
    }
    bool backtrack(vector<vector<char>>& board){
        for(int i = 0; i < board.size(); i++){
            for(int j = 0; j <board.size(); j++){
                if(board[i][j] != '.'){
                    continue;
                }
                // 尝试放置数字
                for(int k = 1; k <= 9; k++){
                    if(isValid(board, i, j, k)){
                        board[i][j] = k + '0';
                        if(backtrack(board)){
                            return true;
                        }
                        board[i][j] = '.';
                    }
                }
                // 这个位置没有可以放置的数字，可以直接返回false
                return false;
            }
        }        
        return true;
    }
    bool isValid(vector<vector<char>>& board, int i, int j, int k){
        // 检查行
        for(int col = 0; col < board.size(); col++){
            if(board[i][col]-'0' == k){
                return false;
            }
        }
        // 检查列
        for(int row = 0; row < board.size(); row++){
            if(board[row][j]-'0' == k){
                return false;
            }
        }
        // 检查九宫格
        int r = i / 3 * 3;
        int c = j / 3 * 3;
        for(int row = r; row < r + 3; row++){
            for(int col = c; col < c + 3; col++){
                if(board[row][col]-'0' == k){
                    return false;
                }
            }
        }
        return true;
    }
};
  • 时间复杂度：$O(9^m)$，$m$ 为棋盘中.的数量。
  • 空间复杂度：$O(9^2)$

字母大小写全排列

分析

  • 递归结束条件：当前索引已到达最后一个字符。
  • 选择条件：每个字母要么翻转，要么不翻转。
  • 补充ASCII码值：
    • 数字0~9：48 ~ 57
    • 大写A~Z：65 ~ 90
    • 小写a~z：97 ~ 122
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public:
    vector<string> letterCasePermutation(string s) {
        string cur = s;
        vector<string> res;
        backtrack(0, cur, res);
        return res;
    }
    void backtrack(int index, string& cur, vector<string>& res){
        // 递归结束
        if(index == cur.length()){
            res.push_back(cur);
            return;
        }
        int type = checkType(cur[index]);
        // 不翻转当前字符
        backtrack(index+1, cur, res);
        // 翻转当前字符
        // 大写变小写
        if(type == 1){
            cur[index] += 32;
            backtrack(index+1, cur, res);
            cur[index] -= 32;
        }
        // 小写变大写
        else if(type == 2){
            cur[index] -= 32;
            backtrack(index+1, cur, res);
            cur[index] += 32;
        }

    }
    int checkType(char ch){
        if(ch >= 48 && ch <= 57){
            return 0;
        }
        if(ch >= 65 && ch <= 90){
            return 1;
        }
        return 2;
    }
};
  • 时间复杂度：$O(n \times 2 ^ n)$
  • 空间复杂度：$O(n \times 2 ^ n)$

火柴拼正方形

拆分字符串使唯一字符串的数目最大

活字印刷

复原IP地址

24点游戏

上面的题以后慢慢刷……

补充

卡特兰数

算法笔记 > 回溯法
#leetcode-notes
0403回溯算法
http://example.com/2024/09/10/posts/0403回溯算法/
作者
Xuan Yang
发布于
2024年9月10日
许可协议