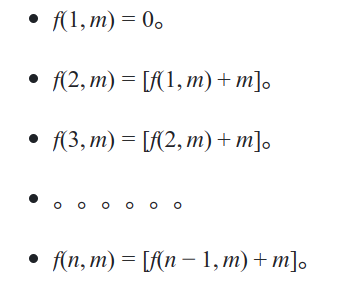0402递归算法

04.02 递归算法

递推过程：指的是将原问题一层一层地分解为与原问题形式相同、规模更小的子问题，直到达到结束条件时停止，此时返回最底层子问题的解。
回归过程：指的是从最底层子问题的解开始，逆向逐一回归，最终达到递推开始时的原问题，返回原问题的解。

具体步骤如下：

  1. 写出递推公式：找到将原问题分解为子问题的规律，并且根据规律写出递推公式。
  2. 明确终止条件：推敲出递归的终止条件，以及递归终止时的处理方法。
  3. 将递推公式和终止条件翻译成代码：
  • 定义递归函数（明确函数意义、传入参数、返回结果等）。
  • 书写递归主体（提取重复的逻辑，缩小问题规模）。
  • 明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。

递归的注意点：

  1. 避免栈溢出：在程序执行中，递归是利用堆栈来实现的。每一次递推都需要一个栈空间来保存调用记录，每当进入一次函数调用，栈空间就会加一层栈帧。每一次回归，栈空间就会减一层栈帧。由于系统中的栈空间大小不是无限的，所以，如果递归调用的次数过多，会导致栈空间溢出。
  2. 避免重复计算：为了避免重复计算，我们可以使用一个缓存（哈希表、集合或数组）来保存已经求解过的f(k)的结果，这也是动态规划算法中的做法。当递归调用用到f(k)时，先查看一下之前是否已经计算过结果，如果已经计算过，则直接从缓存中取值返回，而不用再递推下去，这样就避免了重复计算问题。

509. 斐波那契数

分析

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int fib(int n) {
        // 递归结束
        if(n == 0 || n == 1){
            return n;
        }
        return fib(n-1) + fib(n-2);
    }
};
  • 时间复杂度：$O((\frac{1 + \sqrt{5}}{2})^n)$ 证明过程。
  • 空间复杂度： 调用栈的深度为O(n)。

204. 二叉树的最大深度

分析

写出递推公式：当前二叉树的最大深度 = max(当前二叉树左子树的最大深度, 当前二叉树右子树的最大深度) + 1。

明确终止条件：当前二叉树为空。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == NULL){
            return 0;
        }
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

70. 爬楼梯

分析

写出递推公式：当前方法数等于，跨一级台阶的f(n-1)，加上跨两级台阶的f(n-2)，即f(n) = f(n-1) + f(n-2)，就是斐波那契数列问题。

递归结束条件：n=0,f(0)=0; n=1,f(1)=1。

1
2
3
4
5
6
7
8
9
class Solution {
public:
    int climbStairs(int n) {
        if(n == 0 || n == 1){
            return 1;
        }
        return climbStairs(n-1) + climbStairs(n-2);
    }
};
  • 时间复杂度和空间复杂度与斐波那契数列问题一致。但本题使用这种方法会超出时间限制。

0226. 翻转二叉树

分析

翻转当前节点的左右子树。

递归结束：空节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        // 递归结束
        if(root == NULL){
            return NULL;
        }
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);
        root->left = right;
        root->right = left;
        return root;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

206. 反转链表

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = NULL;
        ListNode* cur = head;
        while(cur){
            ListNode* next = cur->next;
            cur->next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        // 递归结束
        if(!head || !head->next){
            return head;
        }
        ListNode* newHead = reverseList(head->next);
        head->next->next = head;
        head->next = NULL;
        return newHead;
    }
};
  • 时间复杂度：O(n)，其中 n 是链表的长度。需要对链表的每个节点进行反转操作。
  • 空间复杂度：O(n)，其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间，最多为 n 层。

反转链表II

方法1

记录待反转的前一个节点和后一个节点，然后反转，再连接起来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    void reverseList(ListNode* head){
        ListNode *pre = NULL;
        ListNode *cur = head;
        while(cur){
            ListNode* next = cur->next;
            cur->next = pre;
            pre = cur;
            cur = next;
        }
    }
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        // 找到衔接处的节点
        ListNode* dummy = new ListNode(-1);
        dummy->next = head;
        
        ListNode* pre = dummy;
        // pre最终指向left的前一个节点
        for(int i = 0; i < left - 1; i++){
            pre = pre->next;
        }
        // rightNode最终指向right
        ListNode* rightNode = pre;
        for(int i = 0; i < right-left+1; i++){
            rightNode = rightNode->next;
        }
        // 截取链表
        ListNode* leftNode = pre->next;
        ListNode* suc = rightNode->next;
        // 切断链接
        pre->next = NULL;
        rightNode->next = NULL;
        // 反转链表
        reverseList(leftNode);
        // 接回链表
        pre->next = rightNode;
        leftNode->next = suc;
        return dummy->next;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

方法2

方法一的缺点是：如果 left 和 right 的区域很大，恰好是链表的头节点和尾节点时，找到 left 和 right 需要遍历一次，反转它们之间的链表还需要遍历一次，虽然总的时间复杂度为 O(N)，但遍历了链表 2 次。解决：在需要反转的区间里，每遍历到一个节点，让这个新节点来到反转部分的起始位置。

图解反转部分链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        // 设置dummy
        ListNode* dummy = new ListNode(-1);
        dummy->next = head;
        // 记录left的前一个节点
        ListNode* pre = dummy;
        for(int i = 0; i < left - 1; i++){
            pre = pre->next;
        }
        // 在反转区间内
        ListNode* cur = pre->next;
        ListNode* next;
        for(int i = 0; i < right - left; i++){
            next = cur->next;
            cur->next = next->next;
            next->next = pre->next;
            pre->next = next;
        }
        return dummy->next;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

第K个语法符号

递归

$num = (k & 1) \oplus 1 \oplus \lfloor \frac{k+1}{2} \rfloor$

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int kthGrammar(int n, int k) {
        // 递归结束
        if(n == 1){
            return 0;
        }
        return (k & 1) ^ 1 ^ kthGrammar(n-1, (k+1) / 2);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

找规律+递归

每一行的后半部分正好为前半部分的“翻转”——前半部分是 0 后半部分变为 1，前半部分是 1，后半部分变为 0。且每一行的前半部分和上一行相同。我们可以通过「数学归纳法」来进行证明。

对于查询某一个行第 k 个数字，如果 k 在后半部分，那么原问题就可以转化为求解该行前半部分的对应位置的“翻转”数字，又因为该行前半部分与上一行相同，所以又转化为上一行对应对应的“翻转”数字。那么按照这样一直递归下去，并在第一行时返回数字 0 即可。

$1 << (n - 2)$ 是 $2^{n-2}$，表示当前行的前半部分的列数。
如果 k 大于 $2^{n-2}$，那么第 k 列位于当前行的后半部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int kthGrammar(int n, int k) {
        // 递归结束
        if(n == 1){
            return 0;
        }
        if(k > (1 << (n-2))){
            return 1 ^ kthGrammar(n-1, k - (1 << (n-2)));
        }
        return kthGrammar(n-1, k);
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

找规律+位运算

利用 k-1 的二进制表示中 1 的个数来判断符号的值。将 k 转换为 0-based 索引。题目中 k 是从 1 开始的，但我们使用 0-based 索引来简化计算。

k &= k - 1：这是一个经典的位运算技巧，用来清除 k 中最低位的 1。每次执行这个操作，k 中的 1 的个数减少 1。

如果 k - 1 的二进制中 1 的个数是偶数，则翻转了偶数次，结果是 0。
如果 k - 1 的二进制中 1 的个数是奇数，则翻转了奇数次，结果是 1。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int kthGrammar(int n, int k) {
        k--;
        int res = 0;
        while(k > 0){
            k &= k-1;
            res ^= 1;
        }
        return res;
    }
};
  • 时间复杂度：$O(logk)$
  • 空间复杂度：O(1)

反转字符串

分析

可以使用双指针，左指针从第一个元素向后走，右指针从最后一个元素向前走，不断交换左右指针所指元素，直到两指针相撞。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    void reverseString(vector<char>& s) {
        int n = s.size();
        int i = 0;
        int j = n - 1;
        while(i < j){
            swap(s[i], s[j]);
            i++;
            j--;
        }
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

[!NOTE]
为什么把这道题归到递归算法类？

两两交换链表中的结点

分析

定义两个指针，同时还需要保存第一个节点的前驱和第二个节点的后继。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        // 边界条件处理
        if(!head || !head->next){
            return head;
        }

        ListNode* dummy = new ListNode(0);
        dummy->next = head;
        ListNode* pre = dummy;
        ListNode* left = head;
        ListNode* right = left->next;
        while(left && right){
            ListNode* suc = right->next;
            pre->next = right;
            right->next = left;
            left->next = suc;

            pre = left;
            left = suc;
            if(left){
                right = left->next;
            }
        }
        return dummy->next;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

杨辉三角

分析

每一行的第一列和最后一列一定都是1，第i行有i+1个数字，f(0,0) = 1，表示第0行第0列是1。f(i,0)=1，f(i,i)=1,f(i,j) = f(i-1, j-1) + f(i-1, j)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> res;
        res.push_back({1});
        for(int i = 1; i < numRows; i++){
            vector<int> cur(i + 1);
            cur[0] = 1;
            cur[i] = 1;
            // 当前数组应该有i+1个数字
            for(int j = 1; j < i; j++){
                cur[j] = res[i-1][j-1] + res[i-1][j];
            }
            res.push_back(cur);
        }
        return res;
    }
};
  • 时间复杂度：$O(n^2)$
  • 空间复杂度：$O(n^2)$

杨辉三角II

分析

题目提示要用O(rowIndex)的复杂度实现。

组合数$C_n^m = \frac{n!}{m!(n-m)!}$，可推$C_n^{m-1} = \frac{n!}{(m-1)!(n-m+1)!}$，即$C_n^m = C_n^{m-1} \times \frac{n-m+1}{m}$.

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> res(rowIndex + 1);
        res[0] = 1;
        for(int i = 1; i <= rowIndex; i++){
            res[i] = 1ll * res[i-1] * (rowIndex - i + 1) / i;
        }
        return res;
    }
};
  • 时间复杂度：O(rowIndex)
  • 空间复杂度：O(1)，不考虑返回值所占用的空间。

合并两个有序链表

分析

  1. 使用哑节点 dummy 构造一个头节点，并使用 cur 指向 dummy 用于遍历。
  2. 然后判断 list1 和 list2 头节点的值，将较小的头节点加入到合并后的链表中。并向后移动该链表的头节点指针。
  3. 然后重复上一步操作，直到两个链表中出现链表为空的情况。
  4. 将剩余链表链接到合并后的链表中。
  5. 将哑节点dummy的下一个链节点 dummy.next 作为合并后有序链表的头节点返回。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode *dummy = new ListNode(0);
        ListNode *cur = dummy;
        while(list1 && list2){
            if(list1->val <= list2->val){
                cur->next = list1;
                list1 = list1->next;      
            }
            else{
                cur->next = list2;
                list2 = list2->next;
            }
            cur = cur->next;
        }
        // 剩余节点直接链接到后面
        if(list1){
            cur->next = list1;
        }
        if(list2){
            cur->next = list2;
        }
        return dummy->next;

    }
};
  • 时间复杂度：O(n+m)
  • 空间复杂度：O(1)

二叉树中的最大路径和

分析

使用深度优先搜索递归遍历二叉树。递归遍历的同时，维护一个最大路径和变量。计算的结果可能的情况有
2种：

  • 经过空节点的最大贡献值等于 0。
  • 经过非空节点的最大贡献值等于「当前节点值」+「左右子节点的最大贡献值中较大的一个」。
  1. 如果根节点 root 为空，则返回 0。
  2. 递归计算左子树的最大贡献值为 left_max。
  3. 递归计算右子树的最大贡献值为 right_max。
  4. 更新维护最大路径和变量，即 max_sum = max(max_sum, root.val + left_max + right_max)。
  5. 返回以当前节点为根节点，并且经过该节点的最大贡献值。即返回「当前节点值」+「左右子节点的最大贡献值中较大的一个」。
  6. 最终 max_sum 即为答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int res = -INT_MAX;
    int dfs(TreeNode* root){
        if(!root){
            return 0;
        }
        int maxLeft = max(dfs(root->left), 0);
        int maxRight = max(dfs(root->right), 0);
        res = max(res, root->val + maxLeft + maxRight);
        return root->val + max(maxLeft, maxRight);
    }
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return res;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)，取决于递归栈的深度，最大是n。

Pow(x,n)

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    double myPow(double x, int n) {
        long long N = n;
        return N > 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
    }
    double quickMul(double x, long long N){
        if(N == 0){
            return 1.0;
        }
        double y = quickMul(x, N / 2);
        return N % 2 == 0 ? y * y : y * y * x;
    }
};
  • 时间复杂度：O(logn)
  • 空间复杂度：O(logn)

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    double myPow(double x, int n) {
        long long N = n;
        if(N == 0){
            return 1.0;
        }
        if(N < 0){
            x = 1.0 / x;
            N = -N;
        }
        double res = 1.0;
        while(N){
            // 如果N是奇数
            if(N % 2 == 1){
                res *= x;
            }
            x *= x;
            N >>= 1;
        }
        return res;
    }
    double quickMul(double x, long long N){
        if(N == 0){
            return 1.0;
        }
        double y = quickMul(x, N / 2);
        return N % 2 == 0 ? y * y : y * y * x;
    }
};
  • 时间复杂度：O(logn)
  • 空间复杂度：O(1)

不同的二叉搜索树II

分析

分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> dfs(int start, int end){
        // 递归结束
        if(start > end){
            return {NULL};
        }
        // 定义结果
        vector<TreeNode*> res;
        // 枚举可行根节点
        for(int i = start; i <= end; i++){
            vector<TreeNode*> leftTrees = dfs(start, i-1);
            vector<TreeNode*> rightTrees = dfs(i+1, end);
            // 从左子树集合中选出一棵左子树，从右子树集合中选出一棵右子树，拼接到根节点上
            for(auto& left : leftTrees){
                for(auto& right : rightTrees){
                    TreeNode* cur = new TreeNode(i);
                    cur->left = left;
                    cur->right = right;
                    res.push_back(cur);
                }
            }
        }
        return res;
    }
    vector<TreeNode*> generateTrees(int n) {
        if(n == 0){
            return {};
        }
        return dfs(1, n);
    }
};

复杂度分析

破冰游戏

分析

递推公式

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int iceBreakingGame(int num, int target) {
        int res = 0;
        for(int i = 2; i <= num; i++){
            res = (target + res) % i;
        }
        return res;
    }
};
  • 时间复杂度：O(n)
  • 空间复杂度：O(1)

​

算法笔记 > 递归
#leetcode-notes
0402递归算法
http://example.com/2024/08/01/posts/0402递归算法/
作者
Xuan Yang
发布于
2024年8月1日
许可协议