LCR105-LCR112图的搜索

剑指offer（专项突破版）15.2 图的搜索

LCR105.岛屿的最大面积

可以逐一扫描矩阵中的每个格子，如果遇到一个值为1的格子并且它不在之前已知的岛屿上，那么就到达了一个新的岛屿，于是搜索这个岛屿并计算它的面积。在比较所有岛屿的面积之后就可以知道最大的岛屿的面积。

广度优先

广度优先搜索通常需要一个队列。先将起始节点添加到队列中。接下来每步从队列中取出一个节点进行访问。

class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        int maxArea = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1 && !visited[i][j]){
                    int area = getArea(grid, visited, i, j);
                    maxArea = max(maxArea, area);
                }
            }
        }
        return maxArea;
    }
    // 广度优先搜索
    int getArea(vector<vector<int>>& grid, vector<vector<bool>>& visited, int i, int j){
        // 定义一个队列
        queue<pair<int, int>> que;
        que.push(pair<int, int>(i, j));
        visited[i][j] = true;
        // 左右上下四个方向
        vector<pair<int,int>> directions = {{-1,0}, {1,0}, {0,-1}, {0,1}}; 
        // 广度优先
        int area = 0;
        while(!que.empty()){
            pair<int, int> cur = que.front();
            que.pop();
            area++;
            for(auto& dir : directions){
                int r = dir.first + cur.first;
                int c = dir.second + cur.second;
                if(r < grid.size() && r >= 0 && c >= 0 && c < grid[0].size() && grid[r][c] == 1 && !visited[r][c]){
                    que.push(pair<int, int>(r, c));
                    visited[r][c] = true;
                }
            }
        }
        return area;;
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

用栈实现深度优先搜索

这个问题也可以用深度优先搜索解决。如果将前面代码中的队列替换成栈，由于栈按照“后进先出”的顺序进行压栈、出栈操作，因此图搜索的顺序相应地变成深度优先搜索。

class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        int maxArea = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1 && !visited[i][j]){
                    int area = getArea(grid, visited, i, j);
                    maxArea = max(maxArea, area);
                }
            }
        }
        return maxArea;
    }
    // 深度优先搜索
    int getArea(vector<vector<int>>& grid, vector<vector<bool>>& visited, int i, int j){
        // 定义一个栈
        stack<pair<int, int>> st;
        st.push(pair<int, int>(i, j));
        visited[i][j] = true;
        // 左右上下四个方向
        vector<pair<int,int>> directions = {{-1,0}, {1,0}, {0,-1}, {0,1}}; 
        // 深度优先
        int area = 0;
        while(!st.empty()){
            pair<int, int> cur = st.top();
            st.pop();
            area++;
            for(auto& dir : directions){
                int r = dir.first + cur.first;
                int c = dir.second + cur.second;
                if(r < grid.size() && r >= 0 && c >= 0 && c < grid[0].size() && grid[r][c] == 1 && !visited[r][c]){
                    st.push(pair<int, int>(r, c));
                    visited[r][c] = true;
                }
            }
        }
        return area;;
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

基于递归实现深度优先搜索

深度优先搜索还可以用递归代码实现。从起始节点出发的岛屿的面积等于起始节点的面积（一个节点的面积为1）加上与之相邻并且没有访问过的节点能到达的岛屿的面积。求相邻节点能到达的岛屿的面积和初始问题完全一样，可以用递归函数求得。

class Solution {
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        int maxArea = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1 && !visited[i][j]){
                    int area = getArea(grid, visited, i, j);
                    maxArea = max(maxArea, area);
                }
            }
        }
        return maxArea;
    }
    // 深度优先搜索
    int getArea(vector<vector<int>>& grid, vector<vector<bool>>& visited, int i, int j){
        visited[i][j] = true;
        // 左右上下四个方向
        vector<pair<int,int>> directions = {{-1,0}, {1,0}, {0,-1}, {0,1}}; 
        // 深度优先
        int area = 1;
        for(auto& dir : directions){
            int r = dir.first + i;
            int c = dir.second + j;
            if(r < grid.size() && r >= 0 && c >= 0 && c < grid[0].size() && grid[r][c] == 1 && !visited[r][c]){
                visited[r][c] = true;
                area += getArea(grid, visited, r, c);
            }
        }
        return area;
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

LCR106.判断二分图

可以为图中的所有节点着色，两种不同类型的节点分别涂上不同的颜色。如果任意一条边的两个节点都能被涂上不同的颜色，那么整个图就是一个二分图。

利用广度优先搜索对子图着色

可以用广度优先搜索算法搜索与节点i连通的所有节点。广度优先搜索需要一个队列，先将起始节点i添加到队列中。接下来每次从队列中取出一个节点，如果与该节点相邻的节点之前没有访问过，那么相邻的节点被添加到队列中。本题用一个二维数组graph表示图，graph实际上是图的邻接表，与节点i相邻的节点保存在graph[i]中。重复这个过程，直到队列为空，此时与起始节点i连通的所有节点已经搜索完毕。

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        // 对每个节点进行着色
        vector<int> colors(n, -1);
        for(int i = 0; i < n; i++){
            if(colors[i] == -1 && !setColor(graph, colors, i, 0)){
                return false;
            }
        }
        return true;
    }
    bool setColor(vector<vector<int>>& graph, vector<int>& colors, int i, int color){
        // 使用广度优先搜索
        queue<int> que;
        que.push(i);
        colors[i] = color;
        while(!que.empty()){
            int v = que.front();
            que.pop();
            // 对v的每个邻接节点
            for(auto& neighbor : graph[v]){
                // 如果已经着色，判断邻接颜色是否相等
                if(colors[neighbor] >= 0){
                    if(colors[neighbor] == colors[v]){
                        return false;
                    }
                }
                // 否则着色，加入队列
                else{
                    colors[neighbor] = 1 - colors[v];
                    que.push(neighbor);
                }
            }
        }
        return true;
    }
};

• 时间复杂度：O(v+e)
• 空间复杂度：O(v)

利用深度优先搜索对子图着色

深度优先搜索可以用递归代码实现。函数setColor将节点i的颜色设为color。如果该节点在此之前已经着色，并且它的颜色不是color，那么意味着不能按照二分图的规则对图中的节点进行着色，直接返回false。如果此时节点i还没有着色，则将它的颜色设为color，然后给与它相邻的节点涂上颜色1-color。给相邻的节点着色与给节点i着色是相同的问题，可以递归调用函数setColor解决。

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        // 对每个节点进行着色
        vector<int> colors(n, -1);
        for(int i = 0; i < n; i++){
            if(colors[i] == -1 && !setColor(graph, colors, i, 0)){
                return false;
            }
        }
        return true;
    }
    bool setColor(vector<vector<int>>& graph, vector<int>& colors, int i, int color){
        // 使用深度优先搜索
        if(colors[i] >= 0){
            return colors[i] == color;
        }

        colors[i] = color;
        // 对i的每个邻接节点
        for(auto& neighbor : graph[i]){
            if(!setColor(graph, colors, neighbor, 1 - colors[i])){
                return false;
            }
        }
        return true;
    }
};

• 时间复杂度：O(v+e)
• 空间复杂度：O(v)

LCR107.01矩阵

分析

根据题目的要求，上、下、左、右相邻的两个格子的距离为1。可以将图看成一个无权图，图中两个节点的距离是连通它们的路径经过的边的数目。由于这个问题与无权图的最近距离相关，因此可以考虑应用广度优先搜索解决。

广度优先搜索需要一个队列。图中的哪些节点可以当作初始节点添加到队列中？这个问题是求每个格子离最近的0的距离，因此可以将所有的0当作初始节点添加到队列中，然后以值为0的节点作为起点做广度优先搜索。如果经过d步到达某个格子，那么该格子离最近的0的距离就是d。

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int m = mat.size();
        int n = mat[0].size();
        vector<vector<int>> distance(m, vector<int>(n));
        // 使用广度优先搜索
        queue<pair<int, int>> que;
        // 初始化
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(mat[i][j] == 0){
                    que.push(pair<int, int>(i, j));
                    distance[i][j] = 0;
                }
                else{
                    distance[i][j] = INT_MAX;
                }
            }
        }
        // 对每个为0的节点展开搜索
        vector<pair<int, int>> directions = {{-1,0},{1,0},{0,-1},{0,1}};
        while(!que.empty()){
            pair<int, int> pos = que.front();
            que.pop();
            int d = distance[pos.first][pos.second];
            // 对于四个方向
            for(auto& dir : directions){
                int r = pos.first + dir.first;
                int c = pos.second + dir.second;
                // 更新距离
                if(r >= 0 && r < m && c >=0 && c < n){
                    // 将该格子添加到队列中，以便接下来搜索与该格子相连的其他节点
                    if(d + 1 < distance[r][c]){
                        distance[r][c] = d + 1;
                        que.push(pair<int, int>(r, c));
                    }
                }
            }
        }
        return distance;
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

LCR108.单词接龙

单向广度优先搜索

应用图相关算法的前提是找出图中的节点和边。这个问题是关于单词的演变的，所以每个单词就是图中的一个节点。如果两个单词能够相互演变（改变一个单词的一个字母能变成另一个单词），那么这两个单词之间有一条边相连。

这个题目要求计算最短演变序列的长度，即求图中两个节点的最短距离。表示单词演变的图也是一个无权图，按照题目的要求，图中两个节点的距离是连通两个节点的路径经过的节点的数目。通常用广度优先搜索计算无权图中的最短路径，广度优先搜索通常需要用到队列。

为了求得两个节点之间的最短距离，常见的解法是用两个队列实现广度优先搜索算法。一个队列queue1中存放离起始节点距离为d的节点，当从这个队列中取出节点并访问的时候，与队列queue1中节点相邻的节点离起始节点的距离都是d+1，将这些相邻的节点存放到另一个队列queue2中。当队列queue1中的所有节点都访问完毕时，再访问队列queue2中的节点，并将相邻的节点放入queue1中。可以交替使用queue1和queue2这两个队列由近及远地从起始节点开始搜索所有节点。

class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        // 两个队列
        queue<string> que1;
        queue<string> que2;
        // 哈希表
        unordered_set<string> notVisited;
        for(string& word : wordList){
            notVisited.insert(word);
        }
        int len = 1;
        que1.push(beginWord);
        // 广度优先搜索
        while(!que1.empty()){
            // 如果当前单词是endword
            string word = que1.front();
            que1.pop();
            if(word == endWord){
                return len;
            }
            // 否则获取它的所有邻接节点
            vector<string> neighbors = getNeighbors(word);
            for(string& cur : neighbors){
                if(notVisited.find(cur) != notVisited.end()){
                    que2.push(cur);
                    notVisited.erase(cur);
                }
            }
            // 队列1为空
            if(que1.empty()){
                len++;
                que1 = que2;
                clear(que2);
            }
        }
        return 0;
    }
    // 清空队列
    void clear(queue<string>& q) {
        queue<string> empty;
        swap(empty, q);
    }
    // 获取所有邻接节点
    vector<string> getNeighbors(string word){
        vector<string> res;
        // 遍历每一个字符
        for(int i = 0; i < word.length(); i++){
            string cur = word;
            for(char ch = 'a'; ch <= 'z'; ch++){
                if(word[i] != ch){
                    cur[i] = ch;
                    res.push_back(cur);
                }
            }
        }
        return res;
    }
};

• 时间复杂度：$O(N \times C^2)$
• 空间复杂度：$O(N \times C^2)$

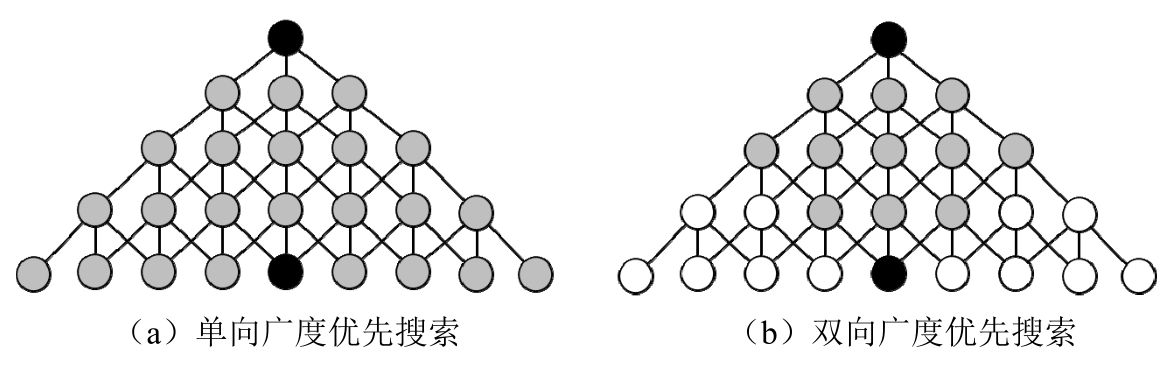
双向广度优先搜索

这个题目是关于单一起始节点、单一目标节点的最短距离问题。前面的解法是从起始节点出发不断朝着目标节点的方向搜索，直到到达目标节点。针对这类问题有一种常见的优化方法，即在从起始节点出发不断朝着目标节点的方向搜索的同时，也从目标节点出发不断朝着起始节点的方向搜索。这种双向搜索的方法能够缩小搜索空间，从而提高搜索的时间效率。

一共使用了3个HashSet，其中，set1和set2分别存放两个方向上当前需要访问的节点，set3用来存放与当前访问的节点相邻的节点。之所以这里用的是HashSet而不是Queue，是因为需要判断从一个方向搜索到的节点在另一个方向是否已经访问过。

先将起始节点beginWord添加到set1中，将目标节点endWord添加到set2中。接下来每次while循环都是从需要访问的节点数目少的方向搜索，这样做是为了缩小搜索的空间。先确保set1中需要访问的节点数更少，接下来访问set1中的每个节点word。如果某个与节点word相邻的节点neighbor在set2中，则说明两个不同方向的搜索相遇，已经找到了一条起始节点和目标节点之间的最短路径，此时路径的长度就是它们之间的最短距离，否则将节点neighbor添加到set3中。当set1中所有的节点都访问完毕，接下来可能会访问set1的节点的相邻节点，即set3中的节点，因此将set1指向set3。然后继续从set1和set2中选择一个节点数目少的方向进行新一轮的搜索。每轮搜索都意味着在起始节点和目标节点之间的最短路径上多前进了一步，因此变量length增加1。

class Solution {
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
        // 两个哈希表
        unordered_set<string> set1;
        unordered_set<string> set2;
        set1.insert(beginWord);
        set2.insert(endWord);
        // 哈希表
        unordered_set<string> notVisited;
        for(string& word : wordList){
            notVisited.insert(word);
        }
        if(notVisited.find(endWord) == notVisited.end()){
            return 0;
        }
        notVisited.erase(endWord);
        int len = 2;
        // 遍历两个set
        while(!set1.empty() && !set2.empty()){
            // set1指向元素更少的集合
            if(set1.size() > set2.size()){
                swap(set1, set2);
            }
            // 存放邻接点的哈希表
            unordered_set<string> set3;
            for(unordered_set<string>::iterator it = set1.begin(); it!=set1.end(); it++){
                string word = *it;
                // 获取所有邻接节点
                vector<string> neighbors = getNeighbors(word);
                for(string& cur : neighbors){
                    // 如果在set2中，说明找到相遇的路径
                    if(set2.find(cur) != set2.end()){
                        return len;
                    }
                    // 否则加入set3
                    if(notVisited.find(cur) != notVisited.end()){
                        set3.insert(cur);
                        notVisited.erase(cur);
                    }
                }
            }
            // set1指向set3
            len++;
            set1 = set3;
        }
        return 0;
    }

    // 获取所有邻接节点
    vector<string> getNeighbors(string word){
        vector<string> res;
        // 遍历每一个字符
        for(int i = 0; i < word.length(); i++){
            string cur = word;
            for(char ch = 'a'; ch <= 'z'; ch++){
                if(word[i] != ch){
                    cur[i] = ch;
                    res.push_back(cur);
                }
            }
        }
        return res;
    }
};

• 时间复杂度：$O(N \times C^2)$
• 空间复杂度：$O(N \times C^2)$

总结

如果面试题要求在无权图中找出两个节点之间的最短距离，那么广度优先搜索可能是更合适的算法。如果面试题要求找出符合条件的路径，那么深度优先搜索可能是更合适的算法。

前面介绍了如何实现树的广度优先搜索和深度优先搜索。树也可以看成图。实际上，树是一类特殊的图，树中一定不存在环。但图不一样，图中可能包含环。

当沿着图中的边搜索一个图时，一定要确保程序不会因为沿着环的边不断在环中搜索而陷入死循环。程序陷入死循环是很多应聘者在解决与图相关的面试题时经常出现的问题。

避免死循环的办法是记录已经搜索过的节点，在访问一个节点之前先判断该节点之前是否已经访问过，如果之前访问过那么这次就略过不再重复访问。

假设一个图有v个节点、e条边。不管是采用广度优先搜索还是深度优先搜索，每个节点都只会访问一次，并且会沿着每条边判断与某个节点相邻的节点是否已经访问过，因此时间复杂度是O（v+e）。

LCR109.打开转盘锁

分析

密码锁4个转轮上的数字定义了密码锁的状态，转动密码锁的转轮可以改变密码锁的状态。一般而言，如果一个问题是关于某事物状态的改变，那么可以考虑把问题转换成图搜索的问题。事物的每个状态是图中的一个节点，如果一个状态能够转变到另一个状态，那么这两个状态对应的节点之间有一条边相连。

对于这个问题而言，密码锁的每个状态都对应着图中的一个节点，如状态”0000”是一个节点，”0001”是另一个节点。如果转动某个转轮一次可以让密码锁从一个状态转移到另一个状态，那么这两个状态之间有一条边相连。例如，将状态”0000”分别向上或向下转动4个转轮中的一个，可以得到8个状态，即”0001”、”0009”、”0010”、”0090”、”0100”、”0900”、”1000”和”9000”，那么图中节点”0000”就有8条边分别和这8个状态对应的节点相连。

由于题目要求的是找出节点”0000”到密码的对应节点的最短路径的长度，因此应该采用广度优先搜索。这是因为广度优先搜索是从起始节点开始首先达到所有距离为1的节点，接着到达所有距离为2节点。广度优先搜索一定是从起始节点沿着最短路径到达目标节点的。

搜索密码锁对应的图时还要注意避开死锁状态对应的节点，因为一旦到达这些节点之后就不能继续向下搜索。

class Solution {
public:
    int openLock(vector<string>& deadends, string target) {
        // 为死亡数字创建一个哈希表，便于检索
        unordered_set<string> dead(deadends.begin(), deadends.end());
        
        // 边界条件，初始密码/目标密码是死亡数字
        string init = "0000";
        if (dead.find(init) != dead.end() || dead.find(target) != dead.end()) {
            return -1;
        }
        
        // 定义一个Visited
        unordered_set<string> visited;
        
        // 定义两个队列，que1存放广度优先搜索的节点，que2存放当前节点的邻接节点
        queue<string> que1;
        
        // 初始化
        visited.insert(init);
        que1.push(init);
        int len = 0;
        
        // 广度优先搜索
        while (!que1.empty()) {
            int size = que1.size();
            for (int i = 0; i < size; i++) {
                string cur = que1.front();
                que1.pop();
                
                // 如果是目标密码
                if (cur == target) {
                    return len;
                }
                
                // 对于所有邻居节点
                vector<string> neighbors = getNeighbors(cur);
                for (string& str : neighbors) {
                    // 判断是否是死亡数字，是否访问过
                    if (dead.find(str) == dead.end() && visited.find(str) == visited.end()) {
                        visited.insert(str);
                        que1.push(str);
                    }
                }
            }
            len++;
        }
        return -1;
    }

    // 找出所有邻居节点
    vector<string> getNeighbors(string cur) {
        vector<string> res;
        for (int i = 0; i < cur.length(); i++) {
            // 向上拨动
            char newCh = cur[i] == '0' ? '9' : cur[i] - 1;
            string newStr = cur;
            newStr[i] = newCh;
            res.push_back(newStr);
            
            // 向下拨动
            newCh = cur[i] == '9' ? '0' : cur[i] + 1;
            newStr[i] = newCh;
            res.push_back(newStr);
        }
        return res;
    }
};

• 时间复杂度：
• 空间复杂度：

LCR110.所有可能得路径

分析

这个题目要求找出有向无环图中从节点0到节点n-1的所有路径，自然需要搜索图中的所有节点。通常可以用广度优先搜索或深度优先搜索完成图的搜索。由于这个题目要求列出从节点0到节点n-1的所有路径，因此深度优先搜索是更合适的选择。

深度优先搜索通常用递归实现。从节点0出发开始搜索。每当搜索到节点i时，先将该节点添加到路径中去。如果该节点正好是节点n-1，那么就找到了一条从节点0到节点n-1的路径。如果不是，则从graph[i]找到每个相邻的节点并用同样的方法进行搜索。当从节点i出发能够抵达的所有节点都搜索完毕之后，将回到前一个节点搜索其他与之相邻的节点。在回到前一个节点之前，需要将节点i从路径中删除。

class Solution {
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        vector<vector<int>> res;
        vector<int> path;
        dfs(0, graph, path, res);
        return res;
    }
    void dfs(int source, vector<vector<int>>& graph, vector<int>& path, vector<vector<int>>& res){
        // 当前节点加入路径
        path.push_back(source);
        // 如果是最后一个节点，即形成一条路径
        if(source == graph.size() - 1){
            res.push_back(path);
        }
        else{
            // 对于每个相连的节点
            for(int next : graph[source]){
                dfs(next, graph, path, res);
            } 
        }
        // 从路径中移除最后的节点
        path.pop_back();
    }
};

• 时间复杂度：$O(n * 2^n)$
• 空间复杂度：O(n)

LCR111.除法求值

分析

class Solution {
public:
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        int n = equations.size();
        // 对于每个节点建立邻接表
        unordered_map<string, vector<pair<string, double>>> graph;
        for(int i = 0; i < n; i++){
            graph[equations[i][0]].push_back({equations[i][1], values[i]});
            graph[equations[i][1]].push_back({equations[i][0], 1 / values[i]});
        }
        // 定义结果数组
        vector<double> res(queries.size(), -1.0);
        for(int i = 0; i < queries.size(); i++){
            if(graph.count(queries[i][0]) && graph.count(queries[i][1])){
                unordered_set<string> visited;
                res[i] = dfs(graph, visited, queries[i][0], queries[i][1], 1.0);
            }
        }
        return res;
    }

    double dfs(unordered_map<string, vector<pair<string, double>>>& graph, unordered_set<string>& visited, string start, string end, double val){
        // 递归结束
        if(start == end){
            return val;
        }
        // 标记已访问过
        visited.insert(start);
        for(auto& node : graph[start]){
            // 如果没访问过
            if(!visited.count(node.first)){
                double cur = dfs(graph, visited, node.first, end, node.second * val);
                // 如果大于 0 肯定可以直接返回，但如果小于 0, 只能说明当前元素作为起点无法与终点连通，应进行下一循环，换个起点
                if(cur > 0){
                    return cur;
                }
            }
        }
        return -1.0;
    }
};

• 时间复杂度：假设有m个查询，则时间复杂度为$O(m \times (v+e))$
• 空间复杂度：图使用邻接表表示，每个节点的邻接表存储相连的节点及其对应的权重。假设图中有V个节点和E条边，那么图的空间复杂度为O(V + E)。使用一个大小为m的结果数组来存储查询结果，所以空间复杂度为O(m)。DFS的递归深度在最坏情况下为图的高度，即最多为V。递归调用栈的空间复杂度为O(V)。使用一个unordered_set来存储访问过的节点，最坏情况下存储所有节点，所以空间复杂度为O(V)。总的空间复杂度为：$O(m+v+e)$。

LCR112.矩阵中的最长递增路径

分析

两个不同数字在图中对应的节点之间的边是有向边，针对这个问题构建出来的图是一个有向图。同时，由于图中所有边都是从较小的数字指向较大的数字，这样的边不可能形成环，因此构建出来的图一定是有向无环图。

接着考虑如何计算图中最长递增路径的长度。由于需要搜索图中的所有节点才能确定最长递增路径的长度，因此这也是一个关于图搜索的问题。解决图搜索通常用广度优先搜索和深度优先搜索这两种不同的方法。这个问题中的路径是非常关键的信息，而深度优先搜索能够很方便地记录搜索的路径，因此深度优先搜索更适合这个问题。

因为不知道从哪个节点开始的递增路径是最长的，所以试着找出从矩阵的每个数字出发的最长递增路径的长度，通过比较可以得出整个矩阵中的最长递增路径的长度。

class Solution {
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        // 定义路径长度数组
        vector<vector<int>> pathLen(m, vector<int>(n, 0));
        int res = 0;
        // 对于每一个节点
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                int len = dfs(matrix, pathLen, i, j);
                res = max(res, len);
            }
        }
        return res;
    }

    int dfs(vector<vector<int>>& matrix, vector<vector<int>>& pathLen, int i, int j){
        // 递归结束
        if(pathLen[i][j] != 0){
            return pathLen[i][j];
        }
        int m = matrix.size();
        int n = matrix[0].size();
        int len = 1;
        vector<pair<int, int>> dirs = {{0,1}, {0,-1}, {1,0}, {-1,0}};
        for(auto& dir : dirs){
            int r = i + dir.first;
            int c = j + dir.second;
            if(r < m && r >= 0 && c < n && c >= 0 && matrix[r][c] > matrix[i][j]){
                int path = dfs(matrix, pathLen, r, c);
                len = max(path+1, len);
            }
        }
        pathLen[i][j] = len;
        return len;
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

总结

如果面试题要求在无权图中找出两个节点之间的最短距离，那么广度优先搜索可能是更合适的算法。如果面试题要求找出符合条件的路径，那么深度优先搜索可能是更合适的算法。