LCR101-LCR104背包问题
剑指offer(专项突破版)14.5 背包问题
LCR101.分割等和子集
分析
如果能够将数组中的数字分成和相等的两部分,那么数组中所有数字的和(记为sum)应该是一个偶数。也可以换一个角度来描述这个问题:能否从数组中选出若干数字,使它们的和等于sum/2(将sum/2记为t)。如果将数组中的每个数字看成物品的重量,也可以这样描述这个问题:能否选择若干物品,使它们刚好放满一个容量为t的背包?由于每个物品(数字)最多只能选择一次,因此这是一个0-1背包问题。
可以用函数f(i,j)表示能否从前i个物品(物品标号分别为0,1,…,i-1)中选择若干物品放满容量为j的背包。如果总共有n个物品,背包的容量为t,那么f(n,t)就是问题的解。
当判断能否从前i个物品中选择若干物品放满容量为j的背包时,对标号为i-1的物品有两个选择。一个选择是将标号为i-1的物品放入背包中,如果能从前i-1个物品(物品标号分别为0,1,…,i-2)中选择若干物品放满容量为j-nums[i-1]的背包(即f(i-1,j-nums[i-1])为true),那么f(i,j)就为true。另一个选择是不将标号为i-1的物品放入背包中,如果从前i-1个物品中选择若干物品放满容量为j的背包(即f(i-1,j)为true),那么f(i,j)也为true。
当j等于0时,即背包的容量为0,不论有多少个物品,只要什么物品都不选择,就能使选中的物品的总重量为0,因此f(i,0)都为true。
当i等于0时,即物品的数量为0,肯定无法用0个物品来放满容量大于0的背包,因此当j大于0时f(0,j)都为false。
1 | |
- 时间复杂度:O(nt)
- 空间复杂度:O(nt)
优化空间效率
如果f(i,j)和f(i-1,j)可以保存到数组的同一个位置,那么只需要一个一维数组。如果按照从左到右的顺序填充表格,f(i-1,j)在计算完f(i,j)之后还可能在计算右边其他值时被用到,那么不能用f(i,j)替换f(i-1,j)。但是如果按照从右到左的顺序填充表格,f(i-1,j)在计算完f(i,j)之后就再也不会被用到,f(i-1,j)被f(i,j)替换掉不会引起任何问题。
1 | |
- 时间复杂度:O(nt)
- 空间复杂度:O(t)
LCR102.目标和
分析
在分析解决这个问题之前,需要先做数学运算。为输入的数组中的有些数字添加“+”,有些数字添加“-”。如果所有添加“+”的数字之和为p,所有添加“-”的数字之和为q,按照题目的要求,p-q=S。如果累加数字中的所有数字,就能得到整个数组的数字之和,记为sum,即p+q=sum。将这两个等式的左右两边分别相加,就可以得到2p=S+sum,即p=(S+sum)/2。
上面的等式表明,如果能够找出数组中和为(S+sum)/2的数字,并给它们添加“+”,然后给其他数字添加“-”,那么最终的计算结果就是S。因此,这个题目等价于计算从数组中选出和为(S+sum)/2的数字的方法的数目。这是和前面的面试题非常类似的题目,是一个典型的0-1背包问题,可以用动态规划解决。
用动态规划求解问题的关键在于确定状态转移方程。可以用函数f(i,j)表示在数组的前i个数字(即nums[0..i-1])中选出若干数字使和等于j的方法的数目。如果数组的长度为n,目标和为t,那么f(n,t)就是整个问题的解。
这个问题的状态转移方程和前面的非常类似,唯一的区别在于这里的f(i,j)的值不再只是一个true或false的标识,而是一个数值。可以用下列等式表示状态转移方程:
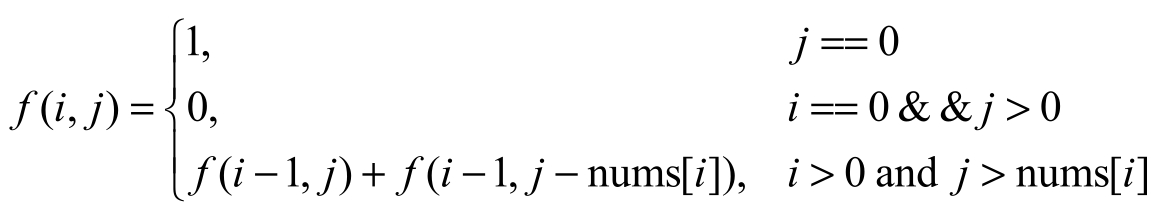
1 | |
- 时间复杂度:O(nt)
- 空间复杂度:O(nt)
优化空间效率
由于计算“dp[i][j]”只需要用上一行“dp[i-1][j]”和“dp[i-1][j-nums[i]]”的值,因此只保存表格中的两行。如果从右向左计算每行的值,f(i,j)和f(i-1,j)就可以保存到同一个位置。因此,只创建一个一维数组dp,按照从右到左的顺序计算,并将f(i-1,j)和f(i,j)都保存到“dp[j]”中。
1 | |
- 时间复杂度:O(nt)
- 空间复杂度:O(t)
LCR103.零钱兑换
分析
每种面额的硬币可以使用任意多次,因此这个问题不再是0-1背包问题,而是一个无界背包问题(也叫完全背包问题)。用函数f(i,j)表示用前i种硬币(coins[0,…,i-1])凑出总额为j需要的硬币的最少数目。当使用0枚标号为i-1的硬币时,f(i,j)等于f(i-1,j)(用前i-1种硬币凑出总额j需要的最少硬币数目,再加上1枚标号为i-1的硬币);当使用1枚标号为i-1的硬币时,f(i,j)等于f(i-1,j-coins[i-1])加1(用前i-1种硬币凑出总额j-coins[i-1]需要的最少硬币数目,再加上1枚标号为i-1的硬币);以此类推,当使用k枚标号为i-1的硬币时,f(i,j)等于f(i-1,j-k×coins[i-1])加k(用前i-1种硬币凑出总额j-k×coins[i-1]需要的最少硬币数目,再加上k枚标号为i-1的硬币)。由于目标是求出硬币数目的最小值,因此f(i,j)是上述所有情况的最小值。该状态转移方程可以用如下等式表示:
f (i,j)=min(f(i-1,j-k×coins[i-1])+k)(k×coins[i-1]≤j)
如果硬币有n种,目标总额为t,那么f(n,t)就是问题的解。
当j等于0(即总额等于0)时,f(i,0)都等于0,即从前i种硬币中选出0个硬币,使总额等于0。当i等于0且j大于0时,即用0种硬币凑出大于0的总额,这显然是不可能的,但可以用一个特殊值表示。
1 | |
- 时间复杂度:O(nt)
- 空间复杂度:O(t)
另一种思路
用函数f(i)表示凑出总额为i的硬币需要的最少数目。需要注意的是,这个函数只有一个参数,表示硬币的总额。如果目标总额为t,那么f(t)就是整个问题的解。
为了凑出总额为i的硬币,有如下选择:在总额为i-coins[0]的硬币中添加1枚标号为0的硬币,此时f(i)等于f(i-coins[0])+1(在凑出总额为i-coins[0]的最少硬币数的基础上加1枚标号为0的硬币);在总额为i-coins[1]的硬币中添加1枚标号为1的硬币,此时f(i)等于f(i-coins[1])+1。以此类推,在总额为i-coins[n-1]的硬币中添加1枚标号为n-1的硬币,此时f(i)等于f(i-coins[n-1])+1。因为目标是计算凑出总额为i的硬币,所以f(i)是上述所有情况的最小值。该状态转移方程可以表示为
f (i)=min(f(i-coins[j])+1)(coins[j]≤i)
显然,f(0)等于0,即凑出总额0至少需要0枚硬币。
1 | |
- 时间复杂度:O(nt)
- 空间复杂度:O(t)
方法一首先遍历每一种硬币,在每次遍历中,尝试将当前硬币加入到已经计算出来的金额组合中,更新最小硬币数。方法二首先遍历每个金额,在每次遍历中,尝试使用每种硬币来更新该金额对应的最小硬币数。
LCR104.组合总和
分析
用f(i)表示和为i的排列的数目。为了得到和为i的排列,有如下选择:在和为i-nums[0]的排列中添加标号为0的数字,此时f(i)等于f(i-nums[0]);在和为i-nums[1]的排列中添加标号为1的数字,此时f(i)等于f(i-nums[1])。以此类推,在和为i-nums[n-1]的排列中添加标号为n-1的数字(n为数组的长度),此时f(i)等于f(i-nums[n-1])。因为目标是求出所有和为i的排列的数目,所以将上述所有情况全部累加起来。该状态转移方程可以表示为
f (i)=∑f (i-nums[j])(nums[j]≤i)
由于只有一个空排列的数字之和等于0,因此f(0)等于1。
1 | |
- 时间复杂度:O(nt)
- 空间复杂度:O(t)

总结
如果解决一个问题需要若干步骤,并且在每个步骤都面临若干选项,不要求列出问题的所有解,而只是要求计算解的数目或找出其中一个最优解,那么这个问题可以应用动态规划加以解决。
本章介绍了单序列问题、双序列问题、矩阵路径问题和背包问题,这几类问题都适合运用动态规划来解决。运用动态规划解决问题的关键在于根据题目的特点推导状态转移方程。一旦确定了状态转移方程,那么问题就能迎刃而解。
状态转移方程是递归表达式,很容易就能将其转换成递归的代码。通常,直接用递归的代码实现状态转移方程存在大量的重复计算,因此需要将计算结果进行缓存,以确保每个值只计算一次。
递归的代码按照自上而下的顺序解决问题,而迭代的代码按照自下而上的顺序解决问题。迭代的代码可以更好地控制计算的顺序,可能会减少缓存所需要的空间复杂度,进一步优化空间效率。