LCR095-LCR097双序列问题

剑指offer（专项突破版）14.3 双序列问题

LCR095.最长公共子序列

分析

由于输入有两个字符串，因此状态转移方程有两个参数。用函数f（i，j）表示第1个字符串中下标从0到i的子字符串（记为s1[0..i]）和第2个字符串中下标从0到j的子字符串（记为s2[0..j]）的最长公共子序列的长度。如果第1个字符串的长度是m，第2个字符串的长度是n，那么f（m-1，n-1）就是整个问题的解。

如果第1个字符串中下标为i的字符（记为s1[i]）与第2个字符串中下标为j（记为s2[j]）的字符相同，那么f（i，j）相当于在s1[0..i-1]和s2[0..j-1]的最长公共子序列的后面添加一个公共字符，也就是f（i，j）=f（i-1，j-1）+1。

如果字符s1[i]与字符s2[j]不相同，则这两个字符不可能同时出现在s1[0..i]和s2[0..j]的公共子序列中。此时s1[0..i]和s2[0..j]的最长公共子序列要么是s1[0..i-1]和s2[0..j]的最长公共子序列，要么是s1[0..i]和s2[0..j-1]的最长公共子序列。也就是说，此时f（i，j）是f（i-1，j）和f（i，j-1）的最大值。

class Solution {
public:
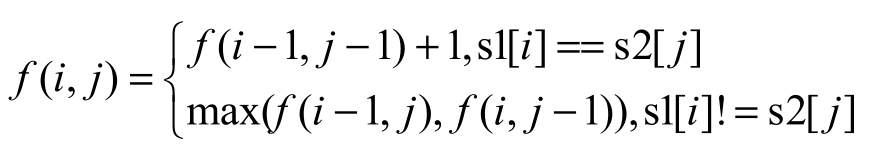
    int longestCommonSubsequence(string text1, string text2) {
        int len1 = text1.length();
        int len2 = text2.length();
        vector<vector<int>> dp(len1+1, vector<int>(len2+1));
        // 填充表格
        for(int i = 0; i < len1; i++){
            for(int j = 0; j < len2; j++){
                if(text1[i] == text2[j]){
                    dp[i+1][j+1] = dp[i][j] + 1;
                }
                else{
                    dp[i+1][j+1] = max(dp[i][j+1], dp[i+1][j]);
                }
            }
        }
        return dp[len1][len2];
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

优化空间效率，只保存表格中的两行

接着尝试优化空间效率。需要注意的是，f（i，j）的值依赖于表格中左上角f（i-1，j-1）的值、正上方f（i-1，j）的值和同一行左边f（i，j-1）的值。由于计算f（i，j）的值时只需要使用上方一行的值和同一行左边的值，因此实际上只需要保存表格中的两行就可以。

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int len1 = text1.length();
        int len2 = text2.length();
        vector<vector<int>> dp(2, vector<int>(len2+1));
        // 填充表格
        for(int i = 0; i < len1; i++){
            for(int j = 0; j < len2; j++){
                if(text1[i] == text2[j]){
                    dp[(i+1)%2][j+1] = dp[i%2][j] + 1;
                }
                else{
                    dp[(i+1)%2][j+1] = max(dp[i%2][j+1], dp[(i+1)%2][j]);
                }
            }
        }
        return dp[len1%2][len2];
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(n)

LCR096.交错字符串

分析

如果字符串s1的长度为m，字符串s2的长度为n，那么它们交织得到的字符串s3的长度一定是m+n。可以用函数f（i，j）表示字符串s1的下标从0到i的子字符串（记为s1[0..i]，长度为i+1）和字符串s2的下标从0到j的子字符串（记为s2[0..j]，长度为j+1）能否交织得到字符串s3的下标从0到i+j+1（记为s3[0..i+j+1]，长度为i+j+2）的子字符串。f（m-1，n-1）就是整个问题的解。

按照字符串的交织规则，字符串s3的下标为i+j+1的字符（s3[i+j+1]）既可能是来自字符串s1的下标为i的字符（s1[i]），也可能是来自字符串s2的下标为j的字符（s2[j]）。如果s3[i+j+1]和s1[i]相同，只要s1[0..i-1]和s2[0..j]能交织得到子字符串s3[i+j]，那么s1[0..i]一定能和s2[0..j]交织得到s3[0..i+j+1]。也就是说，当s3[i+j+1]和s1[i]相同时，f（i，j）的值等于f（i-1，j）的值。类似地，当s3[i+j+1]和s2[j]相同时，f（i，j）的值等于f（i，j-1）的值。如果s1[i]和s2[j]都和s3[i+j+1]相同，此时只要f（i-1，j）和f（i，j-1）有一个值为true，那么f（i，j）的值为true。

由此可知，f（i，j）的值依赖于f（i-1，j）和f（i，j-1）的值。如果i等于0，那么f（0，j）的值依赖于f（-1，j）和f（0，j-1）的值。状态转移方程中的i是指字符串s1中当前处理的子字符串的最后一个字符的下标。当i等于0时，当前处理的字符串s1的子字符串中只有一个下标为0的字符。那么当i等于-1时，当前处理的字符串s1的子字符串中一个字符也没有，是空的。f（-1，j）的含义是当字符串s1的子字符串是空字符串的时候，它和字符串s2从下标从0到j的子字符串（即s2[0..j]）能否交织出字符串s3中下标从0到j的子字符串（即s3[0..j]）。由于空字符和s2[0..j]交织的结果一定还是s2[0..j]，因此f（-1，j）的值其实取决于子字符串s2[0..j]和s3[0..j]是否相同。如果s2[j]和s3[j]不同，那么f（-1，j）的值为false；如果s2[j]和s3[j]相同，那么f（-1，j）的值等于f（-1，j-1）的值。

类似地，f（i，-1）的含义是当字符串s2的子字符串是空字符串时，它和s1[0..i]能否交织得到s3[0..i]，因此f（i，-1）的值取决于子字符串s1[0..i]和s3[0..i]是否相同。如果s1[i]和s3[i]不同，那么f（i，-1）的值为false；如果s1[i]和s3[i]相同，那么f（i，-1）的值等于f（i-1，-1）的值。

当i和j都等于-1时，f（-1，-1）的值的含义是两个空字符串能否交织得到一个空字符串。这显然是可以的，因此f（-1，-1）的值为true。

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        // 边界条件
        int m = s1.length();
        int n = s2.length();
        if(m + n != s3.length()){
            return false;
        }
        // 二维数组存储结果
        vector<vector<bool>> dp(m+1, vector<bool>(n+1));
        dp[0][0] = true;
        // 填充第一行，即s1为空，s2 == s3
        for(int j = 0; j < n && s2[j] == s3[j]; j++){
            dp[0][j+1] = true;
        }
        // 填充第一列，即s2为空，s1 == s3
        for(int i = 0; i < m && s1[i] == s3[i]; i++){
            dp[i+1][0] = true;
        }
        // 填充剩余部分
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                char ch1 = s1[i];
                char ch2 = s2[j];
                char ch3 = s3[i+j+1];
                dp[i+1][j+1] = ((ch1==ch3 && dp[i][j+1]) || (ch2==ch3 && dp[i+1][j]));
            }
        }
        return dp[m][n];
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

优化空间效率

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        // 边界条件
        int m = s1.length();
        int n = s2.length();
        if(m + n != s3.length()){
            return false;
        }
        // 二维数组存储结果
        vector<bool> dp(n+1);
        dp[0] = true;
        // s1为空，s2 == s3
        for(int j = 0; j < n && s2[j] == s3[j]; j++){
            dp[j+1] = true;
        }
        // 填充剩余部分
        for(int i = 0; i < m; i++){
            dp[0] = dp[0] && s1[i] == s3[i];    // s2为空
            for(int j = 0; j < n; j++){
                char ch1 = s1[i];
                char ch2 = s2[j];
                char ch3 = s3[i+j+1];
                dp[j+1] = ((ch1==ch3 && dp[j+1]) || (ch2==ch3 && dp[j]));
            }
        }
        return dp[n];
    }
};

• 时间复杂度：O(mn)
• 空间复杂度：O(n)

LCR097.不同的子序列

分析

由于这个问题的输入有两个字符串，因此状态转移方程有两个参数。用f（i，j）表示字符串S下标从0到i的子字符串（记为S[0..i]）中等于字符串T下标从0到j的子字符串（记为T[0..j]）的子序列的数目。如果字符串S的长度是m，字符串T的长度是n，那么f（m-1，n-1）就是字符串S中等于字符串T的子序列的数目。

当字符串S的长度小于字符串T的长度时，字符串S中不可能存在等于字符串T的子序列，所以当i小于j时f（i，j）的值都等于0。

如果字符串S中下标为i的字符（记为S[i]）等于字符串T中下标为j的字符（记为T[j]），那么对S[i]有两个选择：一个是用S[i]去匹配T[j]，那么S[0..i]中等于T[0..j]的子序列的数目等于S[0..i-1]中等于T[0..j-1]的子序列的数目；另一个是舍去S[i]，那么S[0..i]中等于T[0..j]的子序列的数目等于S[0..i-1]中等于T[0..j]的子序列的数目。因此，当S[i]等于T[j]时，f（i，j）等于f（i-1，j-1）+f（i-1，j）。

如果S[i]和T[j]不相同，则只能舍去S[i]，此时f（i，j）等于f（i-1，j）。

接着考虑字符串S和T为空的情形。由于f（0，j）表示S[0..0]（子字符串的长度为1）中等于T[0..j]的子序列的数目，因此f（-1，j）表示字符串S为空。同理，f（i，-1）表示字符串T为空。

当字符串S、T都为空时，两个字符串匹配，因此f（-1，-1）等于1。如果字符串S为空而字符串T不为空，那么字符串S中不可能存在等于字符串T的子序列，即当j大于或等于0时f（-1，j）等于0。如果字符串S不为空而字符串T为空，那么字符串S的空子序列（舍去字符串S的所有字符）等于字符串T，即当i大于或等于0时f（i，-1）等于1。

class Solution {
public:
    int numDistinct(string s, string t) {
        int m = s.length();
        int n = t.length();
        // 边界条件
        if(m < n){
            return 0;
        }
        vector<vector<unsigned int>> dp(m+1, vector<unsigned int>(n+1));
        dp[0][0] = 1;   // s和t都是空字符串
        
        for(int i = 0; i < m; i++){
            dp[i+1][0] = 1; // 填充第一列，s不为空但t为空
            for(int j = 0; j <= i && j < n; j++){
                // s[i]和t[j]相等，dp[i][j] = dp[i-1][j-1]+dp[i-1][j]
                if(s[i] == t[j]){
                    dp[i+1][j+1] = dp[i][j] + dp[i][j+1];
                }
                else{
                    dp[i+1][j+1] = dp[i][j+1];
                }
            }
        }
        return dp[m][n];
    }
};

注意：dp用int型会溢出。

• 时间复杂度：O(mn)
• 空间复杂度：O(mn)

优化空间效率

由于计算f（i，j）只依赖位于它上一行的f（i-1，j-1）和f（i-1，j），并不依赖位于它左边的f（i，j-1），因此不一定要按照从左到右的顺序计算f（i，j）。如果按照从右到左的顺序，则先计算f（i，j）再计算f（i，j-1）。

class Solution {
public:
    int numDistinct(string s, string t) {
        int m = s.length();
        int n = t.length();
        // 边界条件
        if(m < n){
            return 0;
        }
        vector<unsigned int> dp(n+1);
        dp[0] = 1;   // s和t都是空字符串
        
        for(int i = 0; i < m; i++){
            for(int j = min(i,n-1); j >= 0; j--){
                // s[i]和t[j]相等
                if(s[i] == t[j]){
                    dp[j+1] += dp[j];
                }
                // 省略不相等的时候
            }
        }
        return dp[n];
    }
};

上述代码省略了S[i]和T[j]不相等的情况。在开始计算f（i，j）之前，f（i-1，j）保存在“dp[j+1]”中。当S[i]和T[j]不相等时，f（i，j）等于f（i-1，j）。因此，此时“dp[j+1]”的值也是f（i，j）的值，并不需要任何改动。

• 时间复杂度：O(mn)
• 空间复杂度：O(n)

总结

和单序列问题不同，双序列问题的输入有两个或更多的序列，通常是两个字符串或数组。由于输入是两个序列，因此状态转移方程通常有两个参数，即f（i，j），定义第1个序列中下标从0到i的子序列和第2个序列中下标从0到j的子序列的最优解（或解的个数）。一旦找到了f（i，j）与f（i-1，j-1）、f（i-1，j）和f（i，j-1）的关系，通常问题也就迎刃而解。

由于双序列的状态转移方程有两个参数，因此通常需要使用一个二维数组来保存状态转移方程的计算结果。但在大多数情况下，可以优化代码的空间效率，只需要保存二维数组中的一行就可以完成状态转移方程的计算，因此可以只用一个一维数组就能实现二维数组的缓存功能。