LCR088动态规划的基础知识

剑指offer（专项突破版）14.1 动态规划的基础知识

和适合运用回溯法的问题类似，适用动态规划的问题都存在若干步骤，并且每个步骤都面临若干选择。如果题目要求列举出所有的解，那么很有可能需要用回溯法解决。如果题目是求一个问题的最优解（通常是求最大值或最小值），或者求问题的解的数目（或判断问题是否存在解），那么这个题目有可能适合运用动态规划。

分治法也是采用递归思路把大问题分解成小问题。例如，快速排序算法就是采用分治法。分治法将大问题分解成小问题之后，小问题之间没有重叠的部分。

如果将大问题分解成若干小问题之后，小问题相互重叠，那么直接用递归的代码实现就会存在大量重复计算。小问题之间存在重叠的部分，这是可以运用动态规划求解问题的另一个显著特点。

在用代码实现动态规划的算法时，如果采用递归的代码按照从上往下的顺序求解，那么每求出一个小问题的解就缓存下来，这样下次再遇到相同的小问题就不用重复计算。另一个实现动态规划算法的方法是按照从下往上的顺序，从解决最小的问题开始，并把已经解决的小问题的解存储下来（大部分面试题都存储在一维数组或二维数组中），然后把小问题的解组合起来逐步解决大问题。

LCR088.使用最小花费爬楼梯

分析

爬上一个有多级台阶的楼梯自然需要若干步。按照题目的要求，每次爬的时候既可以往上爬1级台阶，也可以爬2级台阶，也就是每一步都有两个选择。这看起来像是与回溯法有关的问题。但这个问题不是要找出有多少种方法可以爬上楼梯，而是计算爬上楼梯的最少成本，即计算问题的最优解，因此解决这个问题更适合运用动态规划。

分析确定状态转移方程:

$$
f(i) = \begin{cases}
min（f（i-1），f（i-2））+cost[i] & \text{if } i \geq 2 \
cost[i] & \text{if } i < 2
\end{cases}
$$

直接递归

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n = cost.size();
        return min(helper(cost, n-1), helper(cost, n-2));
    }
    int helper(vector<int>& cost, int index){
        if(index < 2){
            return cost[index];
        }
        return min(helper(cost, index-1), helper(cost, index-2)) + cost[index];
    }
};

超出时间限制，无法通过所有测试点。

• 时间复杂度：因为由于重叠子问题，它执行了大量重复的计算，$O(2^n)$
• 空间复杂度：取决于递归调用的深度，在最坏情况下，递归深度可以达到n，每个递归调用都会使用额外的空间来存储其调用栈，因此为$O(n)$.

使用缓存的递归代码

由于执行了大量重复计算，如图所示，计算f(8)和f(7)都要计算f(6)。

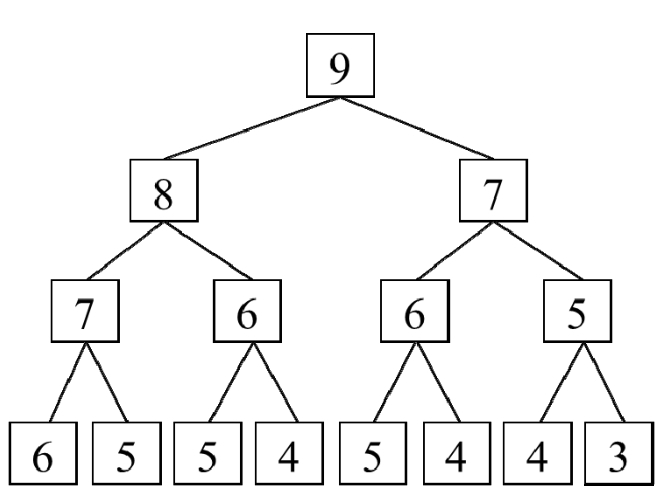
为了避免重复计算带来的问题，一个常用的解决办法是将已经求解过的问题的结果保存下来。在每次求解一个问题之前，应先检查该问题的求解结果是否已经存在。如果问题的求解结果已经存在，则不再重复计算，只需要从缓存中读取之前求解的结果。

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n = cost.size();
        vector<int> dp(n);
        helper(cost, dp, n-1);
        helper(cost, dp, n-2);
        return min(dp[n-1], dp[n-2]);
    }
    void helper(vector<int>&cost, vector<int>& dp, int i){
        if(i < 2){
            dp[i] = cost[i];
        }
        else if(dp[i] == 0){
            helper(cost, dp, i-1);
            helper(cost, dp, i-2);
            dp[i] = min(dp[i-1], dp[i-2]) + cost[i];
        }
    }
};

• 时间复杂度：每个问题f（i）只需要求解一次。如果楼梯有n级台阶，那么上述代码的时间复杂度是O（n）。
• 空间复杂度：需要一个长度为n的数组，因此空间复杂度也是O（n）。

空间复杂度为O（n）的迭代代码

也可以自下而上地解决这个过程，也就是从子问题入手，根据两个子问题f（i-1）和f（i-2）的解求出f（i）的结果。通常用迭代的代码实现自下而上的求解过程。

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n = cost.size();
        vector<int> dp(n);
        dp[0] = cost[0];
        dp[1] = cost[1];
        for(int i = 2; i < n; i++){
            dp[i] = min(dp[i-1], dp[i-2]) + cost[i];
        }
        return min(dp[n-1], dp[n-2]);
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(n)

空间复杂度为O（1）的迭代代码

上述迭代代码还能做进一步的优化。前面用一个长度为n的数组将所有f（i）的结果都保存下来。求解f（i）时只需要f（i-1）和f（i-2）的结果，从f（0）到f（i-3）的结果其实对求解f（i）并没有任何作用。也就是说，在求每个f（i）的时候，需要保存之前的f（i-1）和f（i-2）的结果，因此只要一个长度为2的数组即可。

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n = cost.size();
        int step1 = 0;  // 表示状态 f(i-1)
        int step2 = 0;  // 表示状态 f(i-2)
        int cur = 0;
        for(int i = 2; i <= n; i++){
            cur = min(step1 + cost[i-1], step2 + cost[i-2]);
            step2 = step1;
            step1 = cur;
        }
        return cur;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)

比较四种解法

上面用4种不同的方法解决这个问题。第1种解法在找出状态转移方程之后直接将其转换成递归代码，由于计算过程存在大量的重复计算，因此时间复杂度呈指数级增长，使用这种解法的应聘者通常无法通过编程面试。

第2种解法在第1种解法的基础上添加了一个一维数组，用来缓存已经求解的结果。有了这个长度为O（n）的数组，缓存之后就能够确保每个子问题只需要计算一次，因此时间复杂度是O（n）。

和第2种解法类似，第3种解法的时间复杂度和空间复杂度也都是O（n），但它们有两方面显著的不同。一是求解的顺序不同。第2种解法从大的子问题出发，即采用自上而下的顺序求解；而第3种解法从子问题出发，即采用自下而上的顺序求解。二是代码实现的思路不同。第2种解法采用递归代码实现算法，而第3种解法采用循环代码实现算法。通常，第2种解法和第3种解法都能达到算法面试的要求。

第4种解法在第3种解法的基础上进一步优化空间效率，使空间效率变成O（1）。如果在面试过程中能够想出第4种解法并且能写出正确的代码，那么应聘者毫无疑问能通过这轮面试并为之后的薪资谈判增加砝码。