LCR052-LCR056二叉搜索树

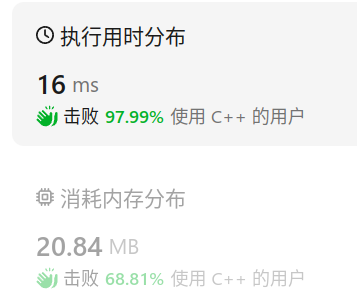
剑指offer（专项突破版）8.3 二叉搜索树

LCR052.展平二叉搜索树

分析

可以通过中序遍历，把一个一个的结点链接到上一个结点的右子树上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* increasingBST(TreeNode* root) {
        TreeNode* newRoot = new TreeNode(0);
        TreeNode* cur = root;
        newRoot->right = cur;
        TreeNode* prev = newRoot;
        // 中序遍历
        stack<TreeNode*> stack;
        while(cur || !stack.empty()){
            // 不断向下直到最左边
            while(cur){
                stack.push(cur);
                cur = cur->left;
            }
            cur = stack.top();
            stack.pop();
            prev->right = cur;
            prev = cur;
            cur->left = NULL;
            cur = cur->right;
        }
        return newRoot->right;
    }
};

LCR052结果

LCR053.二叉搜索树中的中序后继

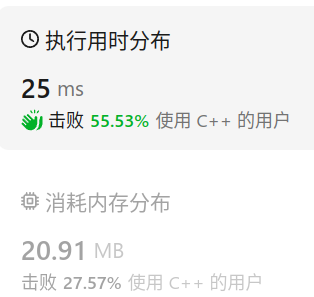
时间复杂度为O(n)的解法

最直观的思路就是采用二叉树的中序遍历。可以用一个布尔变量found来记录已经遍历到节点p。该变量初始化为false，遍历到节点p就将它设为true。在这个变量变成true之后遍历到的第1个节点就是要找的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        stack<TreeNode*> stack;
        TreeNode* cur = root;
        bool flag = false;
        while(cur || !stack.empty()){
            while(cur){
                stack.push(cur);
                cur = cur->left;
            }
            cur = stack.top();
            stack.pop();
            if(flag){
                return cur;
            }
            if(cur == p){
                flag = true;
            }
            cur = cur->right;
        }
        return NULL;
    }
};
  • 时间复杂度：由于中序遍历会逐一遍历二叉树的每个节点，如果二叉树有n个节点，那么这种思路的时间复杂度就是O（n）。
  • 空间复杂度：需要用一个栈保存顺着指向左子节点的指针的路径上的所有节点，因此空间复杂度为O（h），其中h为二叉树的深度。

LCR053方法一结果

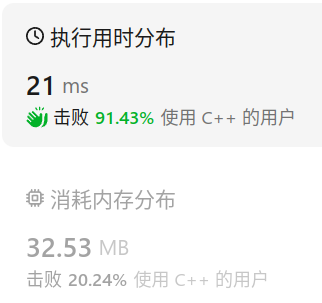
时间复杂度为O(h)的解法

下一个节点的值一定不会小于节点p的值，而且还是大于或等于节点p的值的所有节点中值最小的一个。从根节点开始，每到达一个节点就比较根节点的值和节点p的值。如果当前节点的值小于或等于节点p的值，那么节点p的下一个节点应该在它的右子树。如果当前节点的值大于节点p的值，那么当前节点有可能是它的下一个节点。此时当前节点的值比节点p的值大，但节点p的下一个节点是所有比它大的节点中值最小的一个，因此接下来前往当前节点的左子树，确定是否能找到值更小但仍然大于节点p的值的节点。重复这样的比较，直至找到最后一个大于节点p的值的节点，就是节点p的下一个节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        TreeNode* cur = root;
        TreeNode* res = NULL;
        while(cur){
            if(cur->val > p->val){
                res = cur;
                cur = cur->left;    // 在其左子树上继续查找
            }
            else{
                cur = cur->right;
            }
        }
        return res;
    }
};
  • 时间复杂度：由于while循环每运行一次都会顺着指向左子节点或右子节点的指针前往下一层节点，因此while循环执行的次数等于二叉搜索树的深度。如果把二叉树的深度记为h，那么该算法的时间复杂度为O（h）。
  • 空间复杂度：上述代码除几个变量外没有其他内存开销，因此空间复杂度是O（1）。

LCR053方法二结果

LCR054.把二叉搜索树转换为累加树

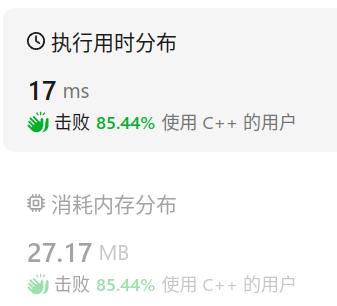
分析

其实就是计算每个节点+其右子树的和。如果能够按照节点值从大到小按顺序遍历二叉搜索树，那么只需要遍历一次就够了，因为遍历到一个节点之前值大于该节点的值的所有节点已经遍历过。通常的中序遍历是先遍历左子树，再遍历根节点，最后遍历右子树，由于左子树节点的值较小，右子树节点的值较大，因此总体上就是按照节点的值从小到大遍历的。如果要按照节点的值从大到小遍历，那么只需要改变中序遍历的顺序，先遍历右子树，再遍历根节点，最后遍历左子树，这样遍历的顺序就颠倒过来了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        stack<TreeNode*> stack;
        TreeNode* cur = root;
        int sum = 0;
        // 按照右根左的顺序遍历
        while(cur || !stack.empty()){
            while(cur){
                stack.push(cur);
                cur = cur->right;
            }
            cur = stack.top();
            stack.pop();
            cur->val += sum;
            sum = cur->val;
            cur = cur->left;
        }
        return root;
    }
};

LCR054结果

LCR055.二叉搜索树迭代器

分析

中序遍历的迭代代码中有一个while循环，循环的条件为true时循环体每执行一次就遍历二叉树的一个节点。当while循环的条件为false时，二叉树中的所有节点都已遍历完。因此，中序遍历的迭代代码中的while循环可以看成迭代器hasNext的判断条件，而while循环体内执行的操作就是函数next执行的操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class BSTIterator {
public:
    TreeNode* cur;
    stack<TreeNode*> stack;
    BSTIterator(TreeNode* root) {
        cur = root;
    }
    
    int next() {
        while(cur){
            stack.push(cur);
            cur = cur->left;
        }
        cur = stack.top();
        stack.pop();
        int res = cur->val;
        cur = cur->right;
        return res;
    }
    
    bool hasNext() {
        return cur != NULL || !stack.empty();
    }
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator* obj = new BSTIterator(root);
 * int param_1 = obj->next();
 * bool param_2 = obj->hasNext();
 */
  • 时间复杂度：函数hasNext的时间复杂度显然是O（1）。如果二叉搜索树有n个节点，调用n次函数next才能遍历完所有的节点，因此函数next的平均时间复杂度是O（1）。
  • 空间复杂度：栈stack的大小为O（h）。由于这个栈一直存在，因此函数hasNext和next的空间复杂度是O（h）。

LCR055结果

LCR056.二叉搜索树中两个节点的值之和

利用哈希表，空间复杂度为O（n）的解法

先进行中序遍历，并把遍历到的值存到哈希表中，然后遍历哈希表，判断是否存在这样的两个数相加等于k。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool findTarget(TreeNode* root, int k) {
        stack<TreeNode*> stack;
        TreeNode* cur = root;
        unordered_map<int, int> hash;
        // 中序遍历
        while(cur || !stack.empty()){
            while(cur){
                stack.push(cur);
                cur = cur->left;
            }
            cur = stack.top();
            if(hash.count(k-cur->val)){
                return true;
            }
            stack.pop();
            hash[cur->val]++;
            cur = cur->right;
        }
        return false;
    }
};
  • 时间复杂度：假设二叉搜索树中节点的数目是n，树的深度为h。上述代码由于需要遍历二叉搜索树，因此时间复杂度是O（n）。
  • 空间复杂度：该算法除了需要一个大小为O（h）的栈保存朝着指向左子节点的指针经过的所有节点，还需要一个大小为O（n）的哈希表保存节点的值，因此总的空间复杂度是O（n）。

LCR056方法一结果

应用双指针，空间复杂度为O（h）的解法

应用上一题的思路，再反向建立一个迭代器。感觉意义不大。

总结

由于中序遍历按照节点值递增的顺序遍历二叉搜索树的每个节点，因此中序遍历是解决二叉搜索树相关面试题最常用的思路。

在普通的二叉树中根据节点值查找对应的节点需要遍历这棵二叉树，因此需要O（n）的时间。但如果是二叉搜索树就可以根据其特性进行优化。如果当前节点的值小于要查找的值，则前往它的右子节点继续查找；如果当前节点的值大于要查找的值，则前往它的左子节点继续查找，这样重复下去直到找到对应的节点为止。如果二叉搜索树的高度为h，那么在二叉搜索树中根据节点值查找对应节点的时间复杂度是O（h）。

算法笔记 > 树
#剑指Offer
LCR052-LCR056二叉搜索树
http://example.com/2024/05/14/posts/LCR052/
作者
Xuan Yang
发布于
2024年5月14日
许可协议