LCR010-LCR013累加数组数字求子数组之和

剑指offer（专项突破版）2.3 累加数组数字求子数组之和

题目链接：LCR010-和为K的子数组

蛮力法：

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int cnt = 0;
        for(int i = 0;i < nums.size();i++){
            int sum = nums[i];
            if(sum == k)
                cnt++;
            for(int j = i+1;j < nums.size();j++){
                sum += nums[j];
                if(sum == k){
                    cnt++;
                }
            }
        }
        return cnt;
    }
};
FORTRAN

时间复杂度分析： $O(n^2)$

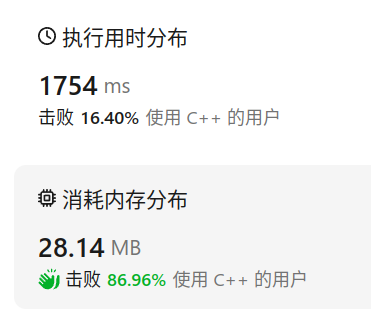
结果：

前缀和+哈希表： 在从头到尾逐个扫描数组中的数字时求出前i个数字之和，并且将和保存下来。数组的前i个数字之和记为x。如果存在一个j（j＜i），数组的前j个数字之和为x-k，那么数组中从第i+1个数字开始到第j个数字结束的子数组之和为k。这个题目需要计算和为k的子数组的个数。当扫描到数组的第i个数字并求得前i个数字之和是x时，需要知道在i之前存在多少个j并且前j个数字之和等于x-k。所以，对每个i，不但要保存前i个数字之和，还要保存每个和出现的次数。分析到这里就会知道我们需要一个哈希表，哈希表的键是前i个数字之和，值为每个和出现的次数。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int sum = 0;    // 记录和
        int cnt = 0;    // 记录结果
        unordered_map<int,int> sumCnt;  // 记录某个和出现的次数
        sumCnt[0] = 1;
        for(int i = 0;i < nums.size();i++){
            sum += nums[i];
            cnt += sumCnt[sum-k];
            sumCnt[sum]++;
        }
        return cnt;
    }
};
AXAPTA

易错点：

遗漏sumCnt[0] = 1：当k就等于当前计算的sum时，如果没有初始化sumCnt[0] = 1，则当前子数组不会被计数上，因为sumCnt[0] = 0。
cnt += sumCnt[sum-k];与sumCnt[sum]++;代码顺序颠倒：如果先进行sumCnt[sum]++;当$k=0$时，计数会出现错误。

时间复杂度分析： O(n)

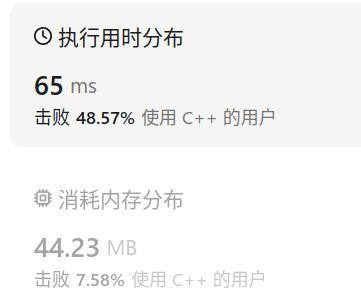
结果：

题目链接：LCR011-连续数组

蛮力法：

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        // 根据题意，找到子数组和为数组长度/2的子数组
        int res = 0;
        // 蛮力法
        for(int i = 0;i < nums.size();i++){
            int sum = nums[i];
            for(int j = i+1;j < nums.size();j++){
                sum += nums[j];
                if(((j-i) % 2) && (sum == (j-i+1)/2) && (j-i+1) > res){  //只有子数组长度为偶数时，0和1的个数才可能相等
                    res = j - i + 1;
                }
            }
        }
        return res;
    }
};
AXAPTA

时间复杂度分析： $O(n^2)$

结果：

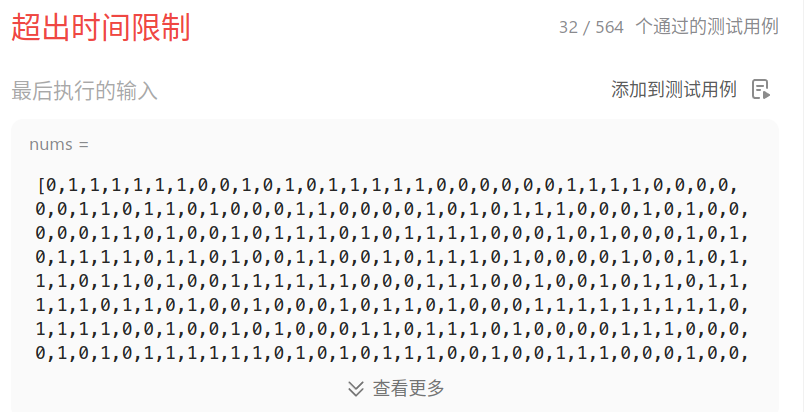
执行超时

前缀和+哈希表：

把数组当中的0变成-1，当扫描到下标为j的数字时，和为m,假设前i个数字的和也是m，则从i+1到j的子数组和为0。用一个哈希表存储前i个数字的和及其下标。

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        // 前缀和+哈希表
        int res = 0;
        unordered_map <int,int> hash;   // 键为前i个数字和，值为i
        int sum = 0;    //记录前缀和
        hash[0] = -1;
        for(int i = 0;i < nums.size();i++){
            sum += nums[i] == 0 ? -1 : 1;
            // 如果存在这样的下标
            if(hash.find(sum) != hash.end()){
                int len = i-hash[sum];       
                if(len > res)
                    res = len;
            }
            else{
                hash[sum] = i;
            }
        } 
        return res;
    }
};
AXAPTA

时间复杂度分析： O(n)

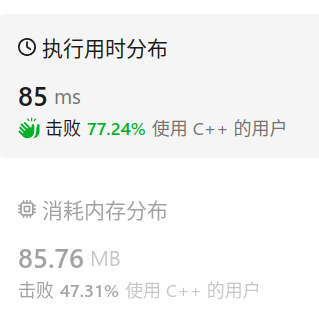
结果：

题目链接：LCR012-寻找数组的中心下标

分析： 假设i为要寻找的下标，则前i-1个数字的和就等于所有数字的和-前i个数字的和。

class Solution {
public:
    int pivotIndex(vector<int>& nums) {
        // 两个循环
        // 求出所有数字的和
        int total = 0;
        for(int i = 0;i < nums.size();i++){
            total += nums[i];
        }
        // 寻找中间下标
        int sum = 0;
        for(int i = 0;i < nums.size();i++){
            sum += nums[i];
            if((sum-nums[i]) == (total-sum)){
                return i;
            }
        }
        return -1;
    }
};
AXAPTA

时间复杂度分析： 上述代码有两个时间复杂度为O（n）的循环，因此总的时间复杂度为O（n）。函数pivotIndex中只用到了若干临时变量，并没有使用数组、哈希表之类的辅助数据容器，因此空间复杂度是O（1）。

结果：

题目链接：LCR013-二维区域和检索 - 矩阵不可变

分析：

假设sums[i][j]表示左上角为（0,0）到右下角（i,j）的子矩阵和，那么从左上角（row1,col1）到右下角（row2,col2）的和为：res = sums[rol2][col2] - sums[row1-1][col2] - sums[rol2][col1-1] + sums[row1-1][col1-1]。
如何求sums[i][j]？可以拆分成两部分，即matrix[i][j]上面的元素sums[i-1][j]以及左边的元素+它本身（每一行按列求和即可）rowSum = matrix[i][0] + ... + matrix[i][j]。
如果输入矩阵的行数和列数分别是m和n，那么辅助数组sums的行数和列数分别为m+1和n+1，这样只是为了简化代码逻辑。如果用公式sums[r2][c2]+sums[r1-1][c2]-sums[r2][c1-1]+sums[r1-1][c1-1]求解左上角坐标为（r1，c1）、右下角坐标为（r2，c2）的子矩阵的数字之和，由于坐标值r1或c1有可能等于0，因此r1-1或c1-1可能是负数，不再是有效的数组下标。如果在矩阵的最上面增加一行，最左面增加一列，这样就不必担心出现数组下标为-1的情形。

class NumMatrix {
public:
    vector<vector<int>> sums;   // 记录前缀和的数组

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();  // m为矩阵行数
        if(m > 0){
            int n = matrix[0].size();   // n为矩阵列数
            sums.resize(m+1,vector<int>(n+1));
            for(int i = 0;i < m;i++){
                int rowSum = 0;
                for(int j = 0;j < n;j++){
                    rowSum += matrix[i][j];
                    sums[i+1][j+1] = sums[i][j+1] + rowSum;
                }
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return sums[row2+1][col2+1] - sums[row1][col2+1] - sums[row2+1][col1] + sums[row1][col1];
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */
MEL

时间复杂度分析： 函数sumRegion用来求子矩阵的数字之和，该函数只是从数组sums中读取几个数字做加法和减法，因此每次调用的时间复杂度都是O（1）。类型NumMatrix的构造函数用来做预处理，根据输入矩阵生成辅助矩阵sums。该构造函数使用两个嵌套的循环计算辅助函数sums中的每个数字，因此时间复杂度是O（mn）。同时，数组sums需要的辅助空间为O（mn）。

结果：

总结

计算前缀和：首先，需要计算数组中每个位置的前缀和，即从数组开头到当前位置的累加和。这可以通过一个循环来完成，将当前位置的值加上前一个位置的前缀和即可得到当前位置的前缀和。
利用前缀和求解子数组之和：在需要求解子数组之和的问题中，利用前缀和可以在常数时间内求得任意子数组的和。通过记录每个前缀和出现的次数，可以在O(1)的时间复杂度内得到某个子数组的和，从而解决了以往使用蛮力法会导致高时间复杂度的问题。
利用哈希表存储前缀和出现的次数：在求解子数组之和的问题中，为了方便查找某个前缀和出现的次数，可以使用哈希表来存储前缀和及其出现的次数。这样，在遍历数组的过程中，可以实时更新哈希表，以便在O(1)时间内获取所需的前缀和信息。
注意边界条件和特殊情况：在使用前缀和方法解题时，需要注意处理边界条件和特殊情况，例如数组为空、特定值等情况，以避免出现错误的结果。
时间复杂度分析：使用前缀和方法解题通常能够将时间复杂度降低至O(n)级别，相比蛮力法的O(n^2)更高效。因此，在面对求解子数组之和、子矩阵之和等问题时，前缀和方法是一种常用且高效的解决方案。

算法笔记 > 数组

#剑指Offer

LCR010-LCR013累加数组数字求子数组之和

http://example.com/2024/04/01/posts/LCR010/

作者

Xuan Yang

发布于

2024年4月1日

许可协议

LCR014-LCR017双指针上一篇

LCR006-LCR009双指针问题下一篇