LCR004.只出现一次的数字

剑指offer（专项突破版）1.2 二进制

题目链接：LCR004-只出现一次的数字

方法1

分析：直接的想法是定义一个map，统计其次数。这里使用unordered_map。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        //定义一个unordered_map，记录出现的数字及其次数
        unordered_map<int, int> dict;
        //遍历
        for(int i = 0; i < nums.size(); i++){
            dict[nums[i]]++;
        }
        //结果
        unordered_map<int, int>::iterator iter;
        for(iter=dict.begin();iter!=dict.end();iter++){
            if(iter->second == 1)
                break;
        }
        return iter->first;
    }
};

时间复杂度分析： 首先，遍历整个输入数组nums并在unordered_map中记录每个数字及其出现的次数。这个过程的时间复杂度为O(n)，其中n是数组nums的大小。接下来，遍历unordered_map以找到出现次数为1的数字。由于unordered_map中最多包含n个不同的数字，因此这个遍历过程的时间复杂度为O(n)。
综上所述，这个算法的总时间复杂度是O(n)。

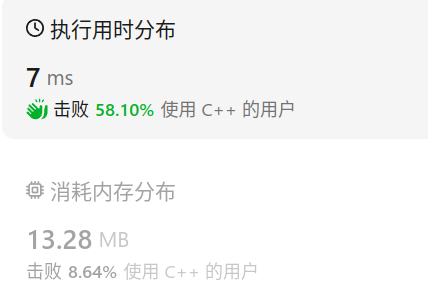
结果：

方法2

这个题目有一个简化版的类似的题目“输入数组中除一个数字只出现一次之外其他数字都出现两次，请找出只出现一次的数字”。任何一个数字异或它自己的结果都是0。如果将数组中所有数字进行异或运算，那么最终的结果就是那个只出现一次的数字。

在这个题目中只有一个数字出现了一次，其他数字出现了3次。相同的3个数字异或的结果是数字本身，但是将数组中所有数字进行异或运算并不能消除出现3次的数字。因此，需要想其他办法。

一个整数是由32个0或1组成的。我们可以将数组中所有数字的同一位置的数位相加。如果将出现3次的数字单独拿出来，那么这些出现了3次的数字的任意第i个数位之和都能被3整除。因此，如果数组中所有数字的第i个数位相加之和能被3整除，那么只出现一次的数字的第i个数位一定是0；如果数组中所有数字的第i个数位相加之和被3除余1，那么只出现一次的数字的第i个数位一定是1。这样只出现一次的任意第i个数位可以由数组中所有数字的第i个数位之和推算出来。当我们知道一个整数任意一位是0还是1之后，就可以知道它的数值。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        //记录每位和的数组，题目规定在int范围内
        int sum[32] = {0};
        //累加
        for(int i = 0;i < nums.size();i++){
            for(int j = 0;j < 32;j++){
                sum[j] += (nums[i] >> (31-j)) & 1;
            }
        }
        //结果
        int res = 0;
        for(int i = 0;i < 32;i++){
            res = (res << 1) + sum[i] % 3;
        }
        return res;
    }
};

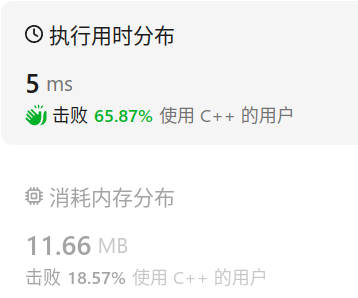
结果：

举一反三

题目：输入一个整数数组，数组中只有一个数字出现m次，其他数字都出现n次。请找出那个唯一出现m次的数字。假设m不能被n整除。

分析：解决面试题4的方法可以用来解决同类型的问题。如果数组中所有数字的第i个数位相加之和能被n整除，那么出现m次的数字的第i个数位一定是0；否则出现m次的数字的第i个数位一定是1。

补充内容

map与unordered_map